在长方体 中,
中, 分别是
分别是 的中点,
的中点, ,过
,过 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
(1)求证: //平面
//平面 ;
;
(2)求 的长;
的长;
(3)在线段 上是否存在点
上是否存在点 ,使直线
,使直线 与
与 垂直,如果存在,求线段
垂直,如果存在,求线段 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
(本小题满分16分)设直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
(1)若 ,求
,求 的范围;
的范围;
(2)若 ,且椭圆上存在一点
,且椭圆上存在一点 其横坐标为
其横坐标为 ,求点
,求点 的纵坐标;
的纵坐标;
(3)若 ,且
,且 ,求椭圆方程.
,求椭圆方程.
(本小题满分16分)设 为正实数,
为正实数, .
.
(1)试比较 的大小;
的大小;
(2)若 ,试证明:以
,试证明:以 为三边长一定能构成三角形;
为三边长一定能构成三角形;
(3)若对任意的正实数 ,不等式
,不等式 恒成立,试求
恒成立,试求 的取值范围.
的取值范围.
(本小题满分15分)今年的国庆假期是实施免收小型客车高速通行费后的第一个重大节假日,有一个自驾游车队。该车队是由31辆车身长都约为5m(以5m计算)的同一车型组成的,行程中经过一个长为2725m的隧道(通过该隧道的车速不能超过25m/s),若车队匀速通过该隧道,设车队的速度为 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当 时,相邻两车之间保持20m的距离;当
时,相邻两车之间保持20m的距离;当 时,相邻两车之间保持
时,相邻两车之间保持 m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为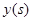 .
.
(1)将 表示为
表示为 的函数;
的函数;
(2)求该车队通过隧道时间 的最小值及此时车队的速度.
的最小值及此时车队的速度.
(本小题满分15分)已知二次函数 .
.
(1)当 时,求不等式
时,求不等式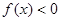 的解集;
的解集;
(2)若不等式 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆 过点
过点 ,离心率
,离心率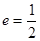 ,
, 为椭圆
为椭圆 上的一点,
上的一点,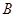 为抛物线
为抛物线 上一点,且
上一点,且 为线段
为线段 的中点.
的中点.
(1)求椭圆 的方程;
的方程;
(2)求直线 的方程.
的方程.