设函数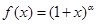 的定义域是
的定义域是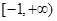 ,其中常数
,其中常数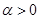 .
.
(1)若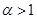 ,求
,求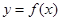 的过原点的切线方程.
的过原点的切线方程.
(2)当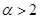 时,求最大实数
时,求最大实数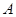 ,使不等式
,使不等式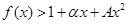 对
对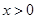 恒成立.
恒成立.
(3)证明当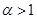 时,对任何
时,对任何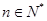 ,有
,有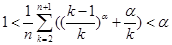 .
.
设函数 的图象如图所示,且与
的图象如图所示,且与 轴相切于原点,若函数的极小值为-4.
轴相切于原点,若函数的极小值为-4.
(1)求 的值;
的值;
(2)求函数 的递减区间.
的递减区间.
中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后
驾车和醉酒驾车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布
直方图.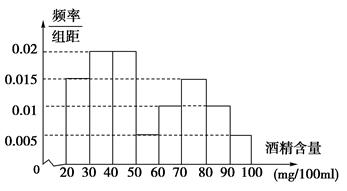
(1)根据频率分布直方图,求此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
已知 是椭圆
是椭圆 上一点,且点
上一点,且点 到椭圆的两个焦点距离之和为
到椭圆的两个焦点距离之和为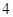 ;
;
(1)求椭圆方程;
(2)设 为椭圆的左顶点,直线
为椭圆的左顶点,直线 交
交 轴于点
轴于点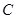 ,过
,过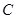 作斜率为
作斜率为 的直线
的直线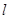 交椭圆于
交椭圆于 两点,若
两点,若 ,求实数
,求实数 的值.
的值.
已知双曲线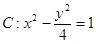 ,
,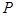 为
为 上任意一点;
上任意一点;
(1)求证:点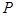 到双曲线
到双曲线 的两条渐近线的距离的乘积是一个常数;
的两条渐近线的距离的乘积是一个常数;
(2)设点 ,求
,求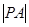 的最小值.
的最小值.
已知圆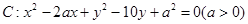 截直线
截直线 的弦长为
的弦长为 ;
;
(1)求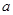 的值;
的值;
(2)求过点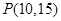 的圆的切线所在的直线方程.
的圆的切线所在的直线方程.