(本题分12分)
如图,斜率为1的直线过抛物线 的焦点,与抛物线交于两点A、B, 将直线
的焦点,与抛物线交于两点A、B, 将直线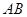 按向量
按向量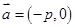 平移得到直线
平移得到直线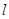 ,
,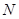 为
为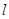 上的动点,
上的动点,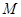 为抛物线弧
为抛物线弧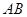 上的动点.
上的动点.
(Ⅰ) 若 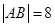 ,求抛物线方程.
,求抛物线方程.
(Ⅱ)求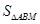 的最大值.
的最大值.
(Ⅲ)求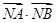 的最小值.
的最小值.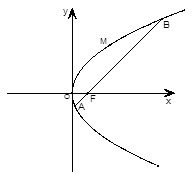
(本题分12分)
如图,在长方体 中,
中,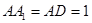 ,
,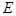 为
为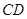 中点.
中点.
(Ⅰ)求证: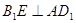 ;
;
(Ⅱ)在棱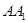 上是否存在一点
上是否存在一点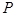 ,使得
,使得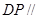 平面
平面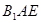 ?若存在,求
?若存在,求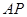 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(Ⅲ)若二面角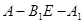 的大小为
的大小为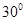 ,求
,求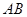 的长.
的长.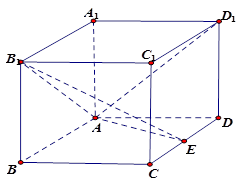
(本题分12分)
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
(Ⅱ)若抽取后不放回,设抽完红球所需的次数为 ,求
,求 的分布列及期望.
的分布列及期望.
(本题分12分)
在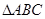 中,角
中,角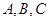 的对边分别为
的对边分别为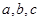 ,
,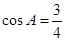 ,
,
(Ⅰ)求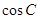 的值;(Ⅱ)若
的值;(Ⅱ)若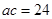 ,求
,求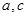 的值.
的值.
(本小题满分15分)已知函数
(1)若函数 在
在 上为增函数,求实数
上为增函数,求实数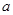 的取值范围;
的取值范围;
(2)当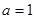 时,求
时,求 在
在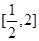 上的最大值和最小值;
上的最大值和最小值;
(3)当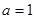 时,求证对任意大于1的正整数
时,求证对任意大于1的正整数 ,
, 恒成立.
恒成立.