(本小题满分13分)如图,设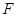 为抛物线
为抛物线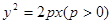 的焦点,
的焦点,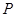 是抛物线上一定点,其
是抛物线上一定点,其
坐为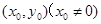 ,
,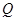 为线段
为线段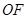 的垂直平分线上一点,且点
的垂直平分线上一点,且点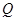 到抛物线的准线
到抛物线的准线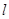 的距离为
的距离为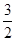 .
.
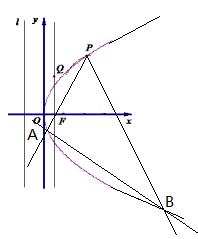
(Ⅰ)求抛物线的方程;
(Ⅱ)过点P任作两条斜率均存在的直线PA、PB,分别与抛物线交于点A、B,如图示,若直线AB的斜率为定值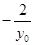 ,求证:直线PA、PB的倾斜角互补.
,求证:直线PA、PB的倾斜角互补.
已知关于 的不等式:
的不等式: 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(1)求整数 的值;(2)在(1)的条件下,解不等式:
的值;(2)在(1)的条件下,解不等式: .
.
(本小题满分9分) 已知极坐标系的极点在直角坐标系的原点处,极轴与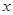 轴的正半轴重合.直线
轴的正半轴重合.直线 的参数方程为:
的参数方程为: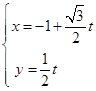 (t为参数),曲线
(t为参数),曲线 的极坐标方程为:
的极坐标方程为: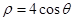 .
.
(Ⅰ)写出 的直角坐标方程,并指出
的直角坐标方程,并指出 是什么曲线;
是什么曲线;
(Ⅱ)设直线 与曲线
与曲线 相交于
相交于 、
、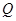 两点,求
两点,求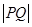 值.
值.
(本小题满分9分)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE= a(0<
a(0< ≦1).
≦1).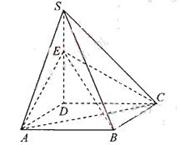
(Ⅰ)求证:对任意的
 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求 的值。
的值。
已知数列 满足
满足
(1)求数列 的通项公式;(2)若数列
的通项公式;(2)若数列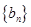 满足
满足 ,求数列
,求数列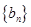 的通项公式;(3)若
的通项公式;(3)若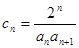 ,求数列
,求数列 的前n项和
的前n项和
已知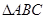 的内角
的内角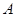 、
、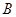 、
、 的对边分别为
的对边分别为 、
、 、
、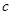 ,
, ,且
,且
(1)求角 ;(2)若向量
;(2)若向量 与
与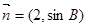 共线,求
共线,求 、
、 的值.
的值.