已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1),求:
(1)a·b,|a+b|;(2)a与b的夹角的余弦值.
(满分13分)已知函数
(1)求 的单调区间;
的单调区间;
(2)记 在区间
在区间
 上的最小值为
上的最小值为 令
令 ;
;
①如果对一切n,不等式 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
②求证:  。
。
(满分12分)如图,在平面直角坐标系中,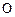 为坐标原点,点
为坐标原点,点 ,
, 且点
且点
 是
是 轴上动点,过点
轴上动点,过点 作线段
作线段 的
的
垂线交 轴于点
轴于点 ,在直线
,在直线 上取点
上取点 ,使
,使 。
。
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)点 是直线
是直线 上的一个动点,
上的一个动点,
过点 作轨迹
作轨迹 的两条切线切点分别为
的两条切线切点分别为 ,
,
求证:
(满分12分)已知数列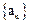 的前n项和为
的前n项和为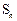 ,对一切正整数n,点
,对一切正整数n,点 都在函数
都在函数 的图像上,且过点
的图像上,且过点 的切线的斜率为
的切线的斜率为 。
。
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列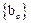 的前n项和
的前n项和 ;
;
(3)数列 满足
满足 ,求数列
,求数列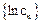 的最值。
的最值。
(满分12分)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面
ABCD为正方形,PD=DC,E、F分别是AB、PB的中点。
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,
并证明你的结论;
(3)求DB与平面DEF所成角的大小。
(满分12分)在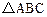 中,已知内角
中,已知内角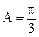 ,边
,边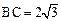 。设内角
。设内角 ,周长为
,周长为 。(1)求函数
。(1)求函数 的解析式和定义域;(2)求
的解析式和定义域;(2)求 的最大值。
的最大值。