已知数列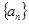 的前
的前 项和为
项和为 ,向量
,向量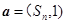 ,
, ,满足条件
,满足条件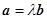 ,
, 且
且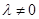 .
.
(1)求数列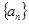 的通项公式;
的通项公式;
(2)设函数 ,数列
,数列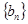 满足条件
满足条件 ,
,
①求数列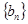 的通项公式;
的通项公式;
②设 ,求数列
,求数列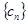 的前
的前 和
和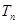 .
.
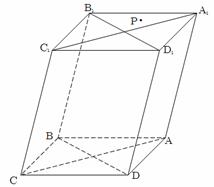
(本小题满分为14分) 如图,过四棱柱 形木块上底面内的一点
形木块上底面内的一点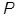 和下底面的对角线
和下底面的对角线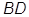 将木块锯开,得到截面
将木块锯开,得到截面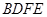 .
.
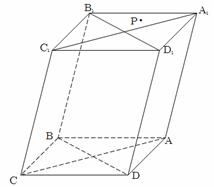
(1)请在木块的上表面作出过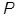 的锯线
的锯线 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形 是矩形时,试证明:平面
是矩形时,试证明:平面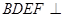 平面
平面 .
.
(本小题满分为14分)已知函数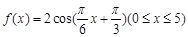 ,点
,点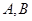 分别是函数
分别是函数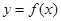
图象上的最高点和最低点.
(1)求点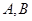 的坐标以及
的坐标以及 的值;
的值;
(2)设点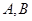 分别在角
分别在角 的终边上,求
的终边上,求 的值.
的值.
(本小题满分10分) 选修4—5:不等式选讲
已知关于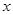 的不等式
的不等式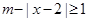 ,其解集为
,其解集为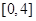 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若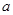 ,
,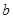 均为正实数,且满足
均为正实数,且满足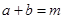 ,求
,求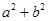 的最小值.
的最小值.
(本小题满分10分) 选修4—4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与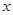 轴的正半轴重合,直线
轴的正半轴重合,直线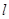 的极坐标方程为:
的极坐标方程为: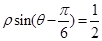 ,曲线
,曲线 的参数方程为:
的参数方程为:
(Ⅰ)写出直线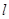 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求曲线 上的点到直线
上的点到直线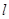 的距离的最大值.
的距离的最大值.
(本小题满分10分) 选修4—1:几何证明选讲
如图,四边形ABCD内接于⊙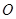 ,过点A作⊙
,过点A作⊙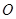 的切线EP交CB的延长线于P,已知
的切线EP交CB的延长线于P,已知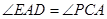 .
.
证明:(Ⅰ)AD=AB;(Ⅱ)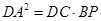 .
.