(本小题满分14分)已知函数 的导函数.
的导函数.
(1)若 ,不等式
,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)解关于x的方程 ;
;
(3)设函数 ,求
,求 时的最小值.
时的最小值.
本题满分16分)
如图,抛物线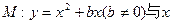 轴交于O,A两点,交直线
轴交于O,A两点,交直线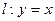 于O,B两点,经过三点O,A,B作圆C。
于O,B两点,经过三点O,A,B作圆C。
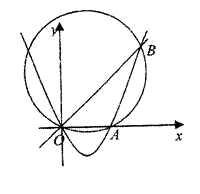
(I)求证:当b变化时,圆C的圆心在一条定直线上;
(II)求证:圆C经过除原点外的一个定点;
(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?

已知圆A: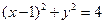 与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
(1)求椭圆的方程;
(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值.
已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1相交于M、N两点.
(1).求实数k的取值范围
(2).求证: 为定值
为定值
(3).若O为坐标原点,且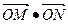 =12,求直线l的方程
=12,求直线l的方程
如图, ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC= CF=2a,DE=a, P为AB的中点.
(1)求证:平面PCF⊥平面PDE;
(2)求证:AE∥平面BCF.
已知两个命题r(x):sinx+cosx>m;s(x):x2+mx+1>0.如果对于任意实数x,r(x)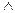 s(x) 为假,r(x)
s(x) 为假,r(x) s(x)为真,求实数m的取值范围。
s(x)为真,求实数m的取值范围。