(本大题满分12分)从某学校的 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于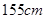 和
和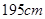 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组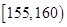 ,第二组
,第二组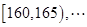 ,第八组
,第八组 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人.
人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在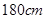 以上(含
以上(含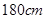 )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为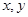 ,事件
,事件 ,事件
,事件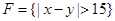 ,求
,求
函数 .
.
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)当 时,求
时,求 的单调区间.
的单调区间.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB= ,
,
如图,O,H分别为AE、AB中点.
(Ⅰ)求证:直线OH//面BDE; (Ⅱ)求证:面ADE
(Ⅱ)求证:面ADE 面ABCE;
面ABCE;
(Ⅲ)求二面角O-DH-E的余弦值.
某次有奖竞猜活动设有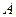 、
、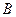 两组相互独立的问题,答对问题
两组相互独立的问题,答对问题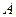 可赢得奖金3000元,答对问题
可赢得奖金3000元,答对问题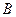 可赢得奖金6000元.规定答题顺序可任选,但只有一个问题答对后才能解答下一个问题,否则中止答题,假设你答对问题
可赢得奖金6000元.规定答题顺序可任选,但只有一个问题答对后才能解答下一个问题,否则中止答题,假设你答对问题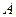 、
、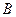 的概率依次为
的概率依次为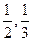 .
.
(Ⅰ)若你按先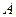 后
后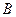 的次序答题,写出你获得奖金的数额
的次序答题,写出你获得奖金的数额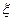 的分布列及期望
的分布列及期望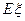 ;
;
(Ⅱ)你认为获得奖金期望的大小与答题顺序有关吗?证明你的结论.
已知函数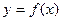 的图像关于直线
的图像关于直线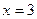 对称,当
对称,当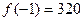 ,且
,且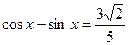 ,
,
求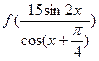 的值.
的值.
设椭圆M: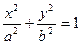 (a>b>0)的离心率为
(a>b>0)的离心率为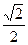 ,长轴长为
,长轴长为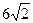 ,设过右焦点F倾
,设过右焦点F倾
斜角为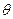 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(2)设过右焦点F且与直线AB垂直的直线交椭圆M于C,D,求|AB| + |CD|的最小
值。