【原创】(本小题满分12分)为调查某市高中男生百米成绩,从该市高中男生中随机抽取20名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组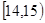 第五组
第五组 ,如图是按上述分组方法得到的频率分布直方图.根据有关规定,成绩小于16秒为达标.
,如图是按上述分组方法得到的频率分布直方图.根据有关规定,成绩小于16秒为达标.

(Ⅰ)求这组数据的众数、中位数及达标率(精确到0.01);
(Ⅱ)从这20人中不达标的人员中任取3人,至少二人成绩在16~17之间的概率.
设
表示数列
的前
项和.
(1)若
为等差数列,推导
的计算公式;
(2)若
,且对所有正整数
,有
.判断
是否为等比数列.
已知向量
, 设函数
.
(1)求
的最小正周期.
(2)求
在
上的最大值和最小值.
设函数 . 为常数且 .
(1)当
时,求
;
(2)若
满足
,但
,则称
为
的二阶周期点.证明函数
有且仅有两个二阶周期点,并求二阶周期点
;
(3)对于(2)中的
,设
,记
的面积为
,求
在区间
上的最大值和最小值。
椭圆
的离心率
.
(1)求椭圆
的方程;
(2)如图,
是椭圆
的顶点,
是椭圆
上除顶点外的任意一点,直线
交
轴于点
,直线
交
于点
.设
的斜率为
,
的斜率为
.证明:
为定值.
如图,直四棱柱 中, , , , , , 为 上一点, ,

(1)证明:
平面
;
(2)求点
到平面
的距离。