(本小题满分12分)已知函数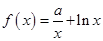 ,其中
,其中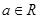 。
。
(Ⅰ)讨论函数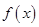 的单调性;
的单调性;
(Ⅱ)若不等式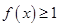 在
在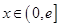 上恒成立,求实数
上恒成立,求实数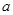 的取值范围。
的取值范围。
某研究小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试的成绩(百分制)如下表所示:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
| 物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
80 |
| 序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
84 |
72 |
83 |
| 物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
82 |
78 |
86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85分(含85分)以上为优秀。
⑴根据上表完成下面的 列联表:
列联表:
| 数学成绩优秀 |
数学成绩不优秀 |
合计 |
|
| 物理成绩优秀 |
|||
| 物理成绩不优秀 |
12 |
||
| 合计 |
20 |
⑵根据⑴中表格的数据计算,有多少的把握,认为学生的数学成绩与物理成绩之间有关系?
某学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数 是一个随机变量,求随机变量
是一个随机变量,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
在平面直角坐标系xOy中,已知曲线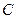 的方程为:
的方程为: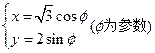 . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,若直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,若直线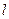 的极坐标方程为
的极坐标方程为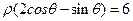 .
.
(Ⅰ)试写出直线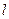 的和曲线
的和曲线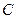 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线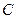 上求一点P,使点P到直线
上求一点P,使点P到直线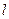 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
在二项式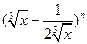 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列. 求展开式的第四项;
求展开式的第四项;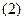 求展开式的常数项;
求展开式的常数项;
在平面直角坐标系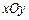 中,已知圆
中,已知圆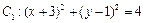 和圆
和圆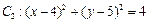 .
.
(1)若直线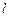 过点
过点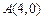 ,且被圆
,且被圆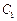 截得的弦长为
截得的弦长为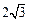 ,求直线
,求直线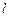 的方程;
的方程;
(2)设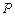 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点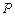 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线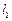 和
和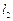 ,它们分别与圆
,它们分别与圆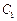 和圆
和圆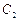 相交,且直线
相交,且直线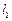 被圆
被圆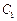 截得的弦长与直线
截得的弦长与直线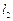 被圆
被圆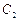 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点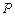 的坐标.
的坐标.