选修4—5: 不等式选讲.
(Ⅰ)设函数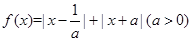 .证明:
.证明: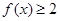 ;
;
(Ⅱ)若实数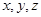 满足
满足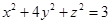 ,求证:
,求证: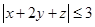
已知 ,
,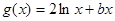 ,且直线
,且直线 与曲线
与曲线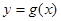 相切.
相切.
(1)若对 内的一切实数
内的一切实数 ,不等式
,不等式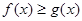 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)(ⅰ)当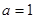 时,求最大的正整数
时,求最大的正整数 ,使得任意
,使得任意 个实数
个实数

 (
( 是自然对数的底数)都有
是自然对数的底数)都有 成立;
成立;
(ⅱ)求证:
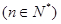 .
.
(1)已知定点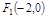 、
、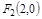 ,动点N满足
,动点N满足 (O为坐标原点),
(O为坐标原点), ,
, ,
,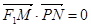 ,求点P的轨迹方程.
,求点P的轨迹方程.
(2)如图,已知椭圆 的上、下顶点分别为
的上、下顶点分别为 ,点
,点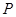 在椭圆上,且异于点
在椭圆上,且异于点 ,直线
,直线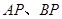 与直线
与直线 分别交于点
分别交于点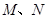 ,
,
(ⅰ)设直线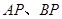 的斜率分别为
的斜率分别为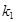 、
、 ,求证:
,求证: 为定值;
为定值;
(ⅱ)当点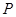 运动时,以
运动时,以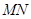 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线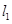 排水管,在路南侧沿直线
排水管,在路南侧沿直线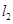 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将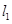 与
与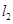 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60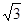 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为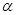 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.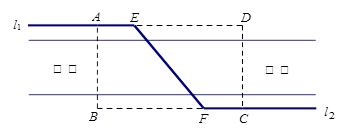
(1)求W关于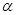 的函数关系式;
的函数关系式;
(2)求W的最小值及相应的角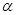 .
.
设集合W是满足下列两个条件的无穷数列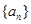 的集合:①对任意
的集合:①对任意 ,
, 恒成立;②对任意
恒成立;②对任意 ,存在与n无关的常数M,使
,存在与n无关的常数M,使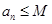 恒成立.
恒成立.
(1)若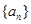 是等差数列,
是等差数列,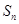 是其前n项和,且
是其前n项和,且 试探究数列
试探究数列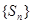 与集合W之间的关系;
与集合W之间的关系;
(2)设数列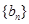 的通项公式为
的通项公式为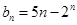 ,且
,且 ,求M的取值范围.
,求M的取值范围.
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB//CD,AB=AD=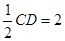 ,点M在线段EC上且不与E、C垂合.
,点M在线段EC上且不与E、C垂合.
(1)当点M是EC中点时,求证:BM//平面ADEF;
(2)当平面BDM与平面ABF所成锐二面角的余弦值为 时,求三棱锥M—BDE的体积.
时,求三棱锥M—BDE的体积.