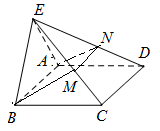
【改编】（本小题满分12分）如图，设四棱锥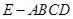
的底面为菱形，且
，
，
．
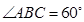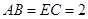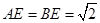（Ⅰ）证明：平面
平面
；
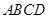（Ⅱ）设M、N分别为EC、ED的中点，求四棱锥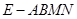
的体积．
（本小题10分）已知函数
．
（1）若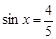
，求函数
的值；
（2）求函数的值域．
（本小题满分12分）在直角坐标系xOy中，以坐标原点O为圆心的圆与直线：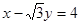
相切．
（Ⅰ）求圆O的方程；
（Ⅱ）圆O与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求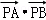
的取值范围．
（本小题满分12分）已知数列{an}满足：Sn=1﹣an（n∈N*），其中Sn为数列{an}的前n项和．
（Ⅰ）试求{an}的通项公式；
（Ⅱ）若数列{bn}满足
，试求{bn}的前n项和公式Tn．
如图，在三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，A1A=AB=2，BC=3．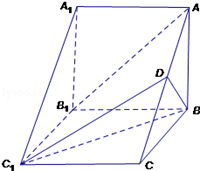
（Ⅰ）求证：AB1∥平面BC1D；
（Ⅱ）求四棱锥B﹣AA1C1D的体积．
（本小题满分12分）设
的内角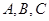
的对边分别为
,
．
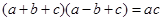（Ⅰ）求
（Ⅱ）若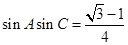
,求