(本小题满分12分)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.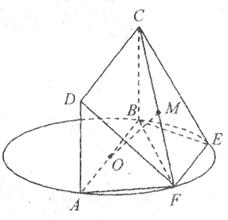
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为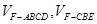 ,求
,求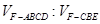 .
.
已知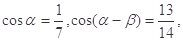 且
且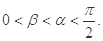
(1)求 的值;
的值;
(2)求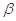 的值。
的值。
已知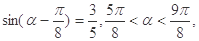 求
求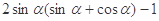 的值。
的值。
在平面直角坐标系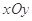 中,已知点
中,已知点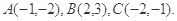
(1)求以线段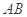 、
、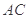 为邻边的平行四边形的两条对角线的长;
为邻边的平行四边形的两条对角线的长;
(2)设实数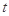 满足
满足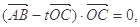 求
求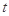 的值。
的值。
假设关于某设备的使用年限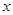 和所支出的维修费用
和所支出的维修费用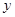 (万元),有如下的统计资料:
(万元),有如下的统计资料:
使用年限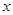 |
2 |
3 |
4 |
5 |
6 |
维修费用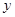 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知道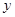 对
对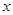 呈线性相关关系.
呈线性相关关系.
附: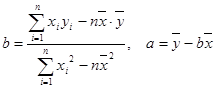
试求:
(1)线性回归方程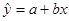 的回归系数.
的回归系数.
(2)估计使用年限为10年时,维修费用是多少?
已知函数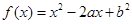 ,
,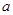 ,
,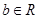 .
.
(1)若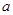 从集合{0,1,2,3}中任取一个元素,
从集合{0,1,2,3}中任取一个元素,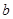 从集合{0,1,2}中任取一个元素,求方程
从集合{0,1,2}中任取一个元素,求方程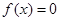 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若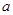 从区间
从区间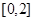 中任取一个数,
中任取一个数,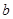 从区间
从区间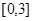 中任取一个数,求方程
中任取一个数,求方程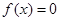 没有实根的概率.
没有实根的概率.