“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动，活动规定：被邀请者要么在24小时内接受挑战，要么选择为慈善机构捐款（不接受挑战），并且不能重复参加该活动．若被邀请者接受挑战，则他需在网络上发布自己被冰水浇遍全身的视频内容，然后便可以邀请另外3个人参与这项活动．假设每个人接受挑战与不接受挑战是等可能的，且互不影响．
（Ⅰ）若某被邀请者接受挑战后，对其他3个人发出邀请，则这3个人中至少有2个人接受挑战的概率是多少？
（Ⅱ）假定（Ⅰ）中被邀请到的3个人中恰有两人接受挑战．根据活动规定，现记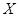
为接下来被邀请到的6个人中接受挑战的人数，求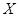的分布列和均值（数学期望）．
某厂拟生产甲、乙两种适销产品，每件利润分别为300、500元，甲、乙产品的部件各自在A、B两个车间分别生产，每件甲、乙产品的部件分别需要A、B车间的生产能力1、2工时；两种产品的部件最后都要在C车间装配，装配每件甲、乙产品分别需要3、4工时.A、B、C三个车间每天可用于生产这两种产品的工时分别为8、12、36，应如何安排生产这两种产品才能获利最多？
设直线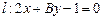
的倾斜角为
.
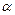（1）若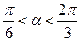
，试求B的取值范围；
（2）若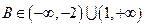
，求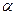
的取值范围.
已知圆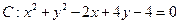
，问是否存在斜率为1的直线
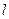，使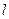被圆C截得弦AB，以AB为直径的圆经过原点，若存在，写出直线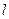的方程；若不存在，说明理由.
如图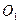，圆
与圆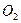
的半径都是1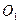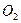，=4，过动点P分别作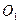圆、圆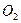的切线PM、PN（M、N分别为切点），使得
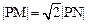，试建立适当的坐标系，并求动点P的轨迹方程.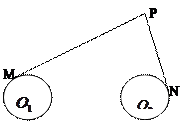
已知圆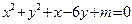
和直线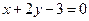
交于P、Q两点且OP⊥OQ（O为坐标原点），求该圆的圆心坐标及半径