已知数列 满足 ,
(1)求 。
(2)由(1)猜想 的通项公式。
(3)用数学归纳法证明(2)的结果。
某校学生会有高一年级6人、高二年级5人、高三年级4人组成,
(1)选其中一人为校学生会主席,则不同的选有多少种;
(2)从3个年级中各选一个人出席一个会议,不同的选法有多少种;
(3)选不同年级的两人参加市里组织的活动,则不同的选法为多少种
已知a,b都是正数,求证: 。
。
(本小题满分12分)
椭圆 与直线
与直线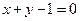 相交于
相交于 、
、 两点,且
两点,且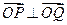 (
(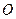 为坐标原点).
为坐标原点).
(Ⅰ)求证: 等于定值;
等于定值;
(Ⅱ)当椭圆的离心率 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
(本小题满分12分)
已知: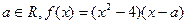
(1)设 的一个极值点。求
的一个极值点。求 在区间
在区间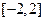 上的最大值和最小值;
上的最大值和最小值;
(2)若 在区间
在区间 上不是单调函数,求
上不是单调函数,求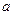 的取值范围。
的取值范围。