阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).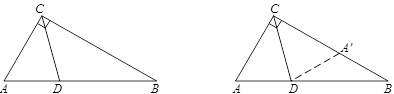
图1 图2
请回答:(1)在图2中,小明得到的全等三角形是△ ≌△ ;
(2)BC和AC、AD之间的数量关系是 .
参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.
求AB的长.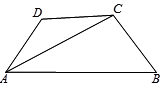
图3
如图,菱形ABCD中,对角线AC、BD交于点O,点P在对角线BD上运动(B、D两点除外),线段PA绕点P顺时针旋转m°(0<m°<180º) 得线段PQ.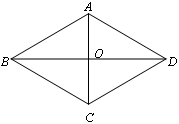
(1)当点Q与点D重合,请在图中用尺规作出点P所处的位置(不写作法,保留作图痕迹);
(2)若点Q落在边CD上(C点除外),且∠ADB=n°.
①探究m与n之间的数量关系;
②当点P在线段OB上运动时,存在点Q,使PQ=QD,直接写出n的取值范围.
某黄金珠宝商店,今年4月份以前,每天的进货量与销售量均为1000克,进入4月份后,每天的进货量保持不变,因国际金价大跌走熊,市场需求量不断增加.如图是4月前后一段时期库存量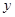 (克)与销售时间
(克)与销售时间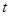 (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算)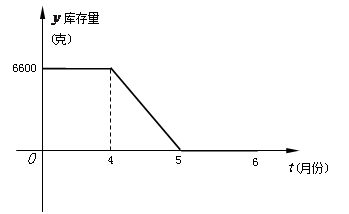
| 商品名称 金 额 |
A |
B |
|||
| 投资金额x(万元) |
x |
5 |
x |
1 |
5 |
| 销售收入y(万元) |
y1=kx (k≠0) |
3 |
y2=ax2+bx(a≠0) |
2.8 |
10 |
(1)该商店月份开始出现供不应求的现象,4月份的平均日销售量为克?
(2)为满足市场需求,商店准备投资20万元同时购进A、B两种新黄金产品。其中购买A、B两种新黄金产品所投资的金额与销售收入存在如图所示的函数对应关系. 请你判断商店这次投资能否盈利?
(3)在(2)的其他条件不变的情况下,商店准备投资m万元同时购进A、B两种新黄金产品,并实现最大盈利3.2万元,请求出m的值.(利润=销售收入-投资金额)
如图(1)是某种台灯的示意图,灯柱BC固定垂直于桌面,AB是转轴,可以绕着点B按顺时针方向转动,AB=10cm,BC=20cm,圆锥形灯罩的轴截面△APQ是等腰直角三角形,∠PAQ=90°,且PQ∥AB.转动前,点A、B、C在同一直线上.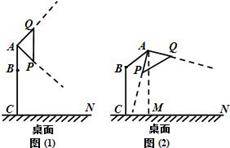
(1)转动AB,如图(2)所示,若灯心A到桌面的距离AM=25cm,求∠ABC的大小;
(2)继续转动AB,当光线AP第一次经过点C,求此时灯心A到桌面的距离AM长.(假设桌面足够大)
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字−1,−2和−3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=-x−1上的概率.
据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图①)、扇形图(图②).
(1)图2中所缺少的百分数是____________;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是______(填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是_____________;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有___________名.