（1）如图1，平面内有一等腰直角三角板ABC（∠ACB=90°）和一直线MN.过点C作CE⊥MN于点E，过点B作BF⊥MN于点F，试证明线段AF，BF，CE之间的数量关系为AF+BF="2CE" 。
（提示：过点C做BF的垂线，利用三角形全等证明。）
（2）若三角板绕点A顺时针旋转至图2的位置，其他条件不变，试猜想线段AF、BF、CE之间的数量关系，并证明你的猜想。
(3)若三角板绕点A顺时针旋转至图3的位置，其他条件不变，则线段AF、BF、CE之间的数量关系为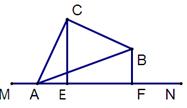 
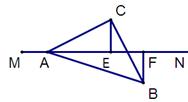
图1 图2 图3
如图，二次函数y＝－x2＋nx＋n2－9（n为常数）的图像经过坐标原点和x轴上另一点A，顶点在第一象限．
(1)求n的值和点A坐标；
(2)已知一次函数y＝－2x＋b(b >0)分别交x轴、y轴于M、N两点．点P是二次函数图像的y轴右侧部分上的一个动点，若PN⊥NM于N点，且△PMN与△OMN相似，求点P坐标．
如图，在平面直角坐标系xOy中，⊙C经过点O，交x轴的正半轴于点B (2，0)，P是
上的一个动点，且∠OPB＝30°.设P点坐标为(m，n)．
(1)当n＝2
，求m的值；
(2)设图中阴影部分的面积为S，求S与n之间的函数关系式，并求S的最大值；
(3)试探索动点P在运动过程中，是否存在整点P(m，n)（横、纵坐标都为整数的点叫整点）?若存在，请求出；若不存在，请说明理由．
如图，折叠矩形ABCD的一边AD使点D落在BC边上的E处，已知折痕AF＝10cm，且tan∠FEC＝
.
(1)求矩形ABCD的面积；
(2)利用尺规作图求作与四边形AEFD各边都相切的⊙O的圆心O（只须保留作图痕迹），并求出⊙O的半径．
已知关于x的一元二次方程x2－2
x＋m＝0有两个不相等的实数根．
(1)求实数m的最大整数值；
(2)在(1)的条件下，方程的实数根是x1，x2（x1>x2），求代数式x1＋2x2的值．
在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4．随机地摸取一个小球后放回，再随机地摸出一个小球，请用列举法（画树状图或列表）求下列事件的概率：
(1)两次取得小球的标号相同；
(2)两次取得小球的标号的和等于4．