已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D。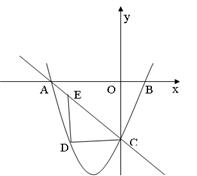
(1)求抛物线的解析式;
(2)当点E的坐标(-2,-1),连接AD,点P在x轴上,使∆APC与∆ADC全等,求出点P的坐标;
(3)当点E在直线AC上运动时,是否存在以D、E、O、C为顶点,OC为一边的平行四边形?若存在,试求出动点E的坐标;若不存在,请说明理由
某商场计划购进冰箱、彩电进行销售,相关信息如下表: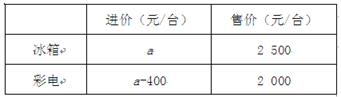
(1)若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等,求表中a的值.
(2)在(1)的条件下,为了满足市场需求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的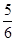 .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.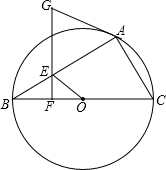
(1)求证:AG与⊙O相切;
(2)若AC=6,AB=8,BE=3,求线段OE的长.
如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方位角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.
(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
2015年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图.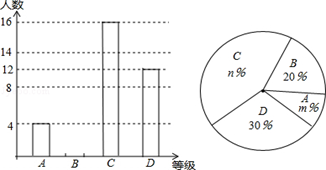
根据图中提供的信息,回答下列问题:
(1)参加演讲比赛的学生共有人,并把条形图补充完整;
(2)扇形统计图中,m=,n=;C等级对应扇形的圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求获A等级的小明参加市比赛的概率.