（年贵州铜仁14分）已知：直线y=ax+b与抛物线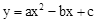
的一个交点为A（0，2），同时这条直线与x轴相交于点B，且相交所成的角β为45°．
（1）求点B的坐标；
（2）求抛物线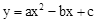的解析式；
（3）判断抛物线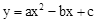与x轴是否有交点，并说明理由．若有交点设为M，N（点M在点N左边），将此抛物线关于y轴作轴反射得到M的对应点为E，轴反射后的像与原像相交于点F，连接NF，EF得△DEF，在原像上是否存在点P，使得△NEP的面积与△NEF的面积相等？若存在，请求出点P的坐标；若不存在，请说明理由．
解方程组
小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤．
妈妈：“今天买这两样菜共花了45元，上月买相同质量的这两样菜只要36元”；
爸爸：“报纸上说了萝卜的单价上涨了50％，排骨的单价上涨了20％”；
小明：“爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少元？”
请你通过列方程（组）求解这天萝卜、排骨的单价（单位：元／斤）．
在“五一”期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话（如图），试根据图中的信息，解答下列问题：
（1）小明他们一共去了几个成人，几个学生？
（2）请你帮助小明算一算，用哪种方式购票更省钱？说明理由．
某油厂从东北调运来的25吨大豆抵达火车站，营业部的王先生准备租用大小两种货车一次性把货物全部运走．已知1辆小货车和2辆大货车一次可以运货10.5吨；2辆小货车和1辆大货车一次可以运货9吨．问：王先生应租大、小两种货车各多少辆才能正好把货物一次全部运走？
某工厂去年的利润为200万元，今年总产值比去年增加20％，总支出比去年减少10％，今年的利润为780万元，问：去年的总支出、总产值各是多少万元？