(年辽宁阜新12分)已知,在矩形ABCD中,连接对角线AC,将△ABC绕点B顺时针旋转90°得到△EFG,并将它沿直线AB向左平移,直线EG与BC交于点H,连接AH,CG.
(1)如图①,当AB=BC,点F平移到线段BA上时,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想;
(2)如图②,当AB=BC,点F平移到线段BA的延长线上时,(1)中的结论是否成立,请说明理由;
(3)如图③,当AB=nBC(n≠1)时,对矩形ABCD进行如已知同样的变换操作,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想.
已知在平面直角坐标系中,点A,B的坐标分别为A(2,-5),
B(5,1).在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出该点的坐标.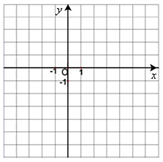
(1)在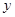 轴上找一点C,使得AC+BC的值最小;
轴上找一点C,使得AC+BC的值最小;
(2)在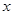 轴上找一点D,使得AD-BD的值最大.
轴上找一点D,使得AD-BD的值最大.
有六张正面分别有数字-3,-1,0,1,5,6的不透明卡片,它们除数字不同外其余全部相同.现将它们背面向上,洗匀后从中任取一张,将该卡片上的数字记为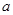 ,求关于
,求关于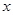 的分式方程
的分式方程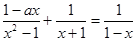 的解,并求该方程的解不小于
的解,并求该方程的解不小于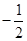 的概率.
的概率.
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.
为响应杭州市政府提出的“文明出行,低碳生活”活动,某校组织了以“文明出行,从我做起”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作品,对其份数与成绩进行整理,制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共1200份,请估计该校学生比赛成绩达到90分以上(包含90分)的作品有多少份.
某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
| 人数m |
0<m≤100 |
100<m≤200 |
m>200 |
| 收费标准(元/人) |
90 |
85 |
75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?