如图，直线AB、CD相交于点O，∠AOD=3∠BOD+20°．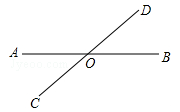
（1）求∠BOD的度数；
（2）以O为端点引射线OE、OF，射线OE平分∠BOD，且∠EOF=90°，求∠BOF的度数，并画图加以说明．
（本小题5分）如图，在图中求作⊙P，使⊙P满足以线段MN为弦，且圆心P到∠AOB两边的距离相等（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）。
（本小题满分10分。每题5分）
（1）计算：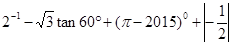
；
（2）解方程：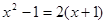
在平面直角坐标系中，矩形OABC的顶点A坐标为（0，3），顶点C坐标为（8，0）．直线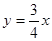
交AB于点D，点P从O点出发，沿射线OD方向以每秒
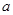个单位长度的速度移动，同时点Q从C点出发沿x轴向原点O方向以每秒1个单位长度的速度移动，当点Q到达O点时，点P停止移动．连结PB，PC，设运动时间为
秒．
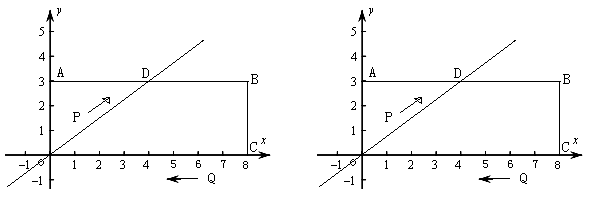
（1）求D点坐标；
（2）当△PBC为等腰三角形时，求P点坐标；
（3）若点P，Q在运动过程中存在某一时刻，使得以点O，P，Q为顶点的三角形与△BCQ相似，求P的运动速度a的值．
如果抛物线C1的顶点在抛物线C2上，同时，抛物线C2的顶点在抛物线C1上，那么，我们称抛物线C1与C2关联．
（1）已知两条抛物线①：y＝x2＋2x－1，②：y＝－x2＋2x＋1，判断这两条抛物线是否关联，并说明理由；
（2）抛物线C1：y＝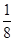
（x＋1）2－2，动点P的坐标为（t，2），将抛物线C1绕点P（t，2）旋转180°得到抛物线C2，若抛物线C2与C1关联，求抛物线C2的解析式．
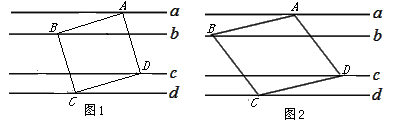
（1）如图1，直线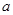
//
//
//
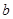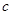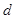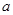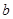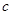，且与，与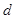之间的距离均为1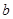，与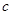之间的距离为2，现将正方形ABCD如图放置，使其四个顶点分别在四条直线上，求正方形的边长；
（2）在（1）的条件下，探究：将正方形ABCD改为菱形ABCD，如图2，当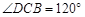
时，求菱形的边长．