（年四川巴中12分）如图，在平面直角坐标系xOy中，抛物线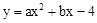
与x轴交于点A
（﹣2，0）和点B，与y轴交于点C，直线x=1是该抛物线的对称轴．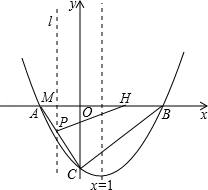
（1）求抛物线的解析式；
（2）若两动点M，H分别从点A，B以每秒1个单位长度的速度沿x轴同时出发相向而行，当点M到达原
点时，点H立刻掉头并以每秒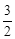
个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点
停止运动，经过点M的直线l⊥x轴，交AC或BC于点P，设点M的运动时间为t秒（t＞0）．求点M的运动时间t与△APH的面积S的函数关系式，并求出S的最大值．
如图，四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥BC于E，若线段AE=5，则S四边形ABCD=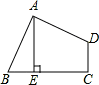
已知二次函数y=x2-2mx+m2-1．
（1）当二次函数的图象经过坐标原点O（0，0）时，求二次函数的解析式；
（2）如图，当m=2时，该抛物线与y轴交于点C，顶点为D，求C、D两点的坐标；
（3）在（2）的条件下，x轴上是否存在一点P，使得PC+PD最短？若P点存在，求出P点的坐标；若P点不存在，请说明理由．
如图，△ABC内接于半圆，AB为直径，过点A作直线MN，若∠MAC=∠ABC．
（1）求证：MN是半圆的切线．
（2）设D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F，求证：FD=FG．
如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC在平面直角坐标系中的位置如图所示．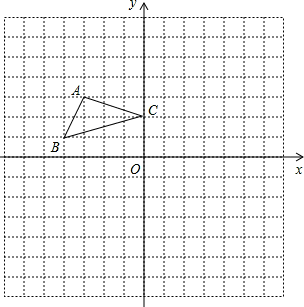
（1）将△ABC向上平移3个单位后，得到△A1B1C1，请画出△A1B1C1，并直接写出点A1的坐标．
（2）将△ABC绕点O顺时针旋转90°，请画出旋转后的△A2B2C2，并求点B所经过的路径长（结果保留x）
黄冈百货商店服装柜在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元．为了迎接“六•一”国际儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽量减少库存．经市场调查发现：如果每件童装降价4元，那么平均每天就可多售出8件．要想平均每天销售这种童装上盈利1200元，那么每件童装应降价多少元？