(年四川资阳12分)如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
先化简,再求值: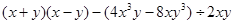 ,其中
,其中 .
.
先化简,再求值: ,其中
,其中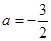 .
.
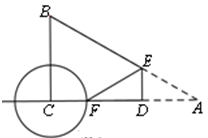
如图,在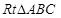 中,
中,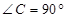 ,
,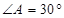 ,
,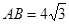 .若动点
.若动点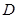 在线段
在线段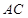 上(不与点
上(不与点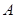 、
、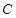 重合),过点
重合),过点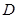 作
作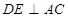 交
交 边于点
边于点 .
.
(1)当点 运动到线段
运动到线段 中点时,
中点时,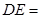 ;
;
(2)点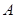 关于点
关于点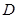 的对称点为点
的对称点为点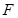 ,以
,以 为半径作⊙
为半径作⊙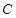 ,当
,当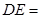 时,⊙
时,⊙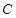 与直线
与直线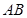 相切.
相切.
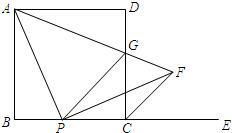
如图,在正方形 中,
中,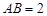 ,点
,点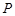 是边
是边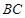 上的任意一点,
上的任意一点,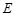 是
是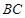 延长线上一点,联结
延长线上一点,联结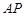 ,作
,作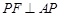 交
交 的平分线
的平分线 上一点
上一点 ,联结
,联结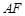 交边
交边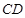 于点
于点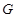 .
.
(1)求证: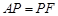 ;
;
(2)设点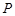 到点
到点 的距离为
的距离为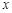 ,线段
,线段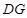 的长为
的长为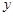 ,试求
,试求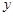 关于
关于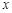 的函数关系式,并写出自变量
的函数关系式,并写出自变量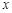 的取值范围;
的取值范围;
(3)当点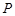 是线段
是线段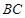 延长线上一动点,那么(2)式中
延长线上一动点,那么(2)式中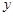 与
与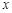 的函数关系式保持不变吗?如改变,试直接写出函数关系式.
的函数关系式保持不变吗?如改变,试直接写出函数关系式.
如图,抛物线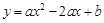 经过点
经过点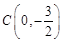 ,且与
,且与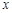 轴交于点
轴交于点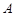 、点
、点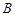 ,若
,若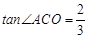 .
.
(1)求此抛物线的解析式;
(2)若抛物线的顶点为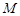 ,点
,点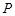 是线段
是线段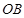 上一动点(不与点
上一动点(不与点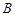 重合),
重合),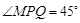 ,射线
,射线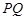 与线段
与线段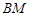 交于点
交于点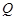 ,当△
,当△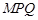 为等腰三角形时,求点
为等腰三角形时,求点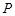 的坐标.
的坐标.