(年陕西省10分)已知抛物线C:y=﹣x2+bx+c经过A(﹣3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.
(1)求抛物线C的表达式;
(2)求点M的坐标;
(3)将抛物线C平移到C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?
先化简再求值:( )÷(x-1),其中x=
)÷(x-1),其中x= .
.
如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,-4).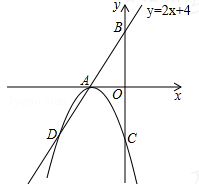
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2 DQ,求点F的坐标.
DQ,求点F的坐标.
综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(-2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.
(1)求抛物线W的解析式及顶点D的坐标;
(2)将抛物线W和▱OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和▱O′A′B′C′,在向下平移的过程中,设▱O′A′B′C′与▱OABC的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线W′的顶点为F,若点M是x轴上的动点,点N是抛物线W′上的动点,试判断是否存在这样的点M和点N,使得以D、F、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?