(年山东聊12分)如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边上异于O,B的一动点,过点M作MN∥AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点M(x,0),△PMN的面积为S.
(1)求出OA所在直线的解析式,并求出点M的坐标为(1,0)时,点N的坐标;
(2)求出S关于x的函数关系式,写出x的取值范围,并求出S的最大值;
(3)若S:S△ANB=2:3时,求出此时N点的坐标.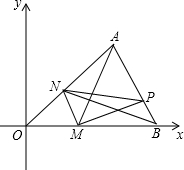
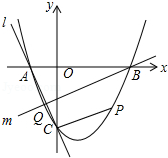
如图,抛物线 与 轴交于 、 两点, 点坐标为 ,与 轴交于点
(1)求抛物线的解析式;
(2)点 在抛物线位于第四象限的部分上运动,当四边形 的面积最大时,求点 的坐标和四边形 的最大面积.
(3)直线 经过 、 两点,点 在抛物线位于 轴左侧的部分上运动,直线 经过点 和点 ,是否存在直线 ,使得直线 、 与 轴围成的三角形和直线 、 与 轴围成的三角形相似?若存在,求出直线 的解析式,若不存在,请说明理由.
如图,在 中, 为直角, , ,半径为2的动圆圆心 从点 出发,沿着 方向以1个单位长度 秒的速度匀速运动,同时动点 从点 出发,沿着 方向也以1个单位长度 秒的速度匀速运动,设运动时间为 秒 以 为圆心, 长为半径的 与 、 的另一个交点分别为 、 ,连接 、 .
(1)当 为何值时,点 与点 重合?
(2)当 经过点 时,求 被 截得的弦长.
(3)若 与线段 只有一个公共点,求 的取值范围.

如图,在矩形 中,点 在边 上,且 ,过点 作 ,垂足为点
(1)求证: ;
(2)以 为圆心, 长为半径作圆弧交 于点 ,若 ,求扇形 的面积.(结果保留

某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价 元收费;若每月用水量超过14吨,则超过部分每吨按市场价 元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为 吨,应交水费为 元,请写出 与 之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
如图,在平面直角坐标系中, 为坐标原点, 的边 垂直与 轴,垂足为点 ,反比例函数 的图象经过 的中点 ,且与 相交于点 , , ,
(1)求反比例函数 的解析式;
(2)求 的值;
(3)求经过 、 两点的一次函数解析式.
