（年浙江金华12分）如图，直角梯形ABCO的两边OA，OC在-优题课

（年浙江金华12分）如图，直角梯形ABCO的两边OA，OC在坐标轴的正半轴上，BC∥x轴，OA=OC=4，以直线x=1为对称轴的抛物线过A，B，C三点.
（1）求该抛物线线的函数解析式.
（2）已知直线l的解析式为，它与x轴的交于点G，在梯形ABCO的一边上取点P.
①当m=0时，如图1，点P是抛物线对称轴与BC的交点，过点P作PH⊥直线l于点H，连结OP，试求△OPH的面积.
②当时，过P点分别作x轴、直线l的垂线，垂足为点E，F. 是否存在这样的点P，使以P，E，F为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由.

科目数学题型解答题难度中等

如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系 $x O y$ ，规定一个单位长度代表1米．E $（ 0 ， 8 ）$ 是抛物线的顶点．

（1）求此抛物线对应的函数表达式；

（2）在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点 $P_{1} ， P_{4}$ 在x轴上，MN与矩形 $P_{1} P_{2} P_{3} P_{4}$ 的一边平行且相等．栅栏总长l为图中粗线段 $P_{1} P_{2} ， P_{2} P_{3} ， P_{3} P_{4} ，$ MN长度之和，请解决以下问题：

（ⅰ）修建一个“”型栅栏，如图2，点 $P_{2} ， P_{3}$ 在抛物线AED上．设点P₁的横坐标为 $m （ 0 ＜ m \leq 6 ）$ ，求栅栏总长l与m之间的函数表达式和l的最大值；

（ⅱ）现修建一个总长为18的栅栏，有如图3所示的“”型和“”型两种设计方案，请你从中选择一种，求出该方案下矩形 $P_{1} P_{2} P_{3} P_{4}$ 面积的最大值，及取最大值时点P₁的横坐标的取值范围（P₁在P₄右侧）．

已知四边形ABCD中， $B C ＝ C D$ ，连接BD，过点C作BD的垂线交AB于点E，连接DE．

（1）如图1，若 $D E ∥ B C$ ，求证：四边形BCDE是菱形；

（2）如图2，连接AC，设BD，AC相交于点F，DE垂直平分线段AC．

（ⅰ）求∠CED的大小；

（ⅱ）若 $A F ＝ A E$ ，求证： $B E ＝ C F$ ．

第24届冬奥会于2022年2月20日在北京胜利闭幕．某校七、八年级各有 $500$ 名学生，为了解这两个年级学生对本次冬奥会的关注程度，现从这两个年级各随机抽取 $n$ 名学生进行冬奥会知识测试，将测试成绩按以下六组进行整理（得分用 $x$ 表示）：

A： $70 \leq x ＜ 75$ ，B： $75 \leq x ＜ 80$ ，C： $80 \leq x ＜ 85$ ，

D： $85 \leq x ＜ 90$ ，E： $90 \leq x ＜ 95$ ，F： $95 \leq x \leq 100$ ，

并绘制七年级测试成绩频数分布直方图和八年级测试成绩扇形统计图，部分信息如下：

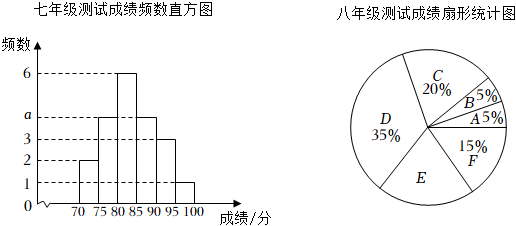
已知八年级测试成绩D组的全部数据如下：

$86 ， 85 ， 87 ， 86 ， 85 ， 89 ， 88$ ．

请根据以上信息，完成下列问题：

（1） $n$ ＝＿＿＿＿， $a$ ＝＿＿＿＿；

（2）八年级测试成绩的中位数是＿＿＿＿；

（3）若测试成绩不低于 $90$ 分，则认定该学生对冬奥会关注程度高．请估计该校七、八两个年级对冬奥会关注程度高的学生一共有多少人，并说明理由．

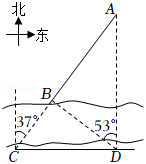
如图，为了测量河对岸A，B两点间的距离，数学兴趣小组在河岸南侧选定观测点C，测得A，B均在C的北偏东 $37 °$ 方向上，沿正东方向行走90米至观测点D，测得A在D的正北方向，B在D的北偏西 $53 °$ 方向上．求A，B两点间的距离．

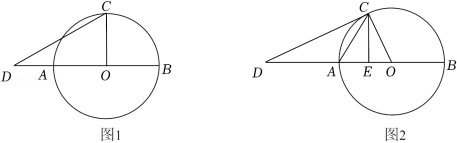
参考数据： $\sin 37 ° \approx 0.60 ， \cos 37 ° \approx 0.80 ， \tan 37 ° \approx 0.75$ ．

已知AB为⊙O的直径，C为⊙O上一点，D为BA的延长线上一点，连接CD．

（1）如图1，若 $C O ⊥ A B$ ， $∠ D ＝ 30 ° ， O A ＝ 1$ ，求AD的长；

（2）如图2，若DC与⊙O相切，E为OA上一点，且 $∠ A C D ＝ ∠ A C E$ ．求证： $C E ⊥ A B$ ．