(年黑龙江牡丹江农垦10分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
已知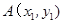 ,
,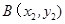 是反比例函数
是反比例函数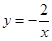 图象上的两点,且
图象上的两点,且 ,
,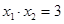 .
.
(1)在图中用“描点”的方法作出此反比例函数的图象;
(2)求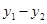 的值及点
的值及点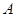 的坐标;
的坐标;
(3)若-4<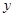
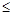 -1,依据图象写出
-1,依据图象写出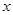 的取值范围.
的取值范围.
如图,已知抛物线的对称轴为直线 :
: 且与
且与 轴交于点
轴交于点 与
与 轴交于点
轴交于点
 .
.
(1)求抛物线的解析式;
(2)试探究在此抛物线的对称轴 上是否存在一点
上是否存在一点 ,使
,使 的值最小?若存在,求
的值最小?若存在,求 的最小值,若不存在,请说明理由;
的最小值,若不存在,请说明理由;
(3)以 为直径作⊙
为直径作⊙ ,过点
,过点 作直线
作直线 与⊙
与⊙ 相切于点
相切于点 ,
, 交
交 轴于点
轴于点 ,求直线
,求直线 的解析式.
的解析式.
如图,在△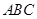 中,
中,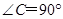 ,
,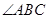 的平分线
的平分线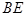 交
交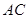 于点
于点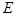 ,过点
,过点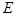 作直线
作直线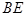 的垂线交
的垂线交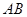 于点
于点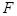 ,⊙
,⊙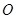 是△
是△ 的外接圆.
的外接圆.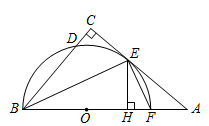
(1)求证: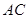 是⊙
是⊙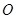 的切线;
的切线;
(2)过点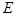 作
作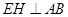 于点
于点 ,求证:
,求证: .
.
甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、丙两位同学的概率;
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
随着市民环保意识的增强,节庆期间烟花爆竹销售量逐年下降.某市2011年销售烟花爆竹20万箱,到2013年烟花爆竹销售量为9.8万箱.求该市2011年到2013年烟花爆竹年销售量的平均下降率.