(年福建三明14分)如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(﹣2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.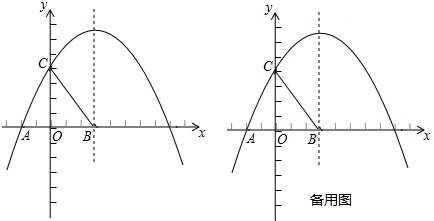
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;
(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.
为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图),请你用尺规作图的方法确定点P的位置.(要求: 写出已知、求作;不写作法,保留作图痕迹,必须用铅笔作图)
如图,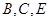 三点在同一条直线上,
三点在同一条直线上, ∥
∥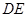 ,
, 。求证:△ABC≌△CDE。
。求证:△ABC≌△CDE。
解方程: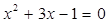
如图,已知直线 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
(1)填空:点A的坐标为,点B的坐标为,AB的长为.
(2)求点C、D的坐标
(3)求抛物线的解析式
(4)若抛物线与正方形沿射线AB下滑,直至点C落在
 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为.
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为.
(本题满分12分) 为了让广大青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动可以锻炼人的灵活性,增强人的爆发力.因此小明和小亮在课外活动中报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补齐下面的表格;
| 第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
|
| 小明 |
13.3 |
13.4 |
13.3 |
13.3 |
|
| 小亮 |
13.2 |
13.1 |
13.5 |
13.3 |
(2)分别计算他们的平均数、极差和方差填入下表,若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
| 平均数 |
极差 |
方差 |
|
| 小明 |
13.3 |
0.004 |
|
| 小亮 |
0.4 |