(年湖北随州10分)已知两条平行线l1、l2之间的距离为6,截线CD分别交l1、l2于C、D两点,一直角的顶点P在线段CD上运动(点P不与点C、D重合),直角的两边分别交l1、l2与A、B两点.
(1)操作发现
如图1,过点P作直线l3∥l1,作PE⊥l1,点E是垂足,过点B作BF⊥l3,点F是垂足.此时,小明认为△PEA∽△PFB,你同意吗?为什么?
(2)猜想论证
将直角∠APB从图1的位置开始,绕点P顺时针旋转,在这一过程中,试观察、猜想:当AE满足什么条件时,以点P、A、B为顶点的三角形是等腰三角形?在图2中画出图形,证明你的猜想.
(3)延伸探究
在(2)的条件下,当截线CD与直线l1所夹的钝角为150°时,设CP=x,试探究:是否存在实数x,使△PAB的边AB的长为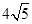 ?请说明理由.
?请说明理由.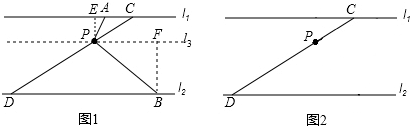
(本小题满分10分)
有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中E组所在的扇形的圆心角为144°
被抽取的体育测试成绩频数分布表
| 组别 |
成绩 |
频数 |
| A |
20<x≤24 |
2 |
| B |
24<x≤28 |
3 |
| C |
28<x≤32 |
5 |
| D |
32<x≤36 |
b |
| E |
36<x≤40 |
20 |
| 合计 |
a |

根据上面的图表提供的信息,回答下列问题:
(1)计算频数分布表中a与b的值;
(2)请估计该校九年级学生这次体育测试成绩的平均分(结果取整数)
(3)小敏测得扇形统计图的半径为5,将扇形统计图的A,B,C区域块剪下来,剩余部分卷成圆锥体(不算重合部分),则圆锥体的高为多少?
(本小题满分8分)某一空间图形的三视图如右图所示, 其中主视图:半径为1的半圆以及高为1的矩形; 左视图:半径为1的圆以及高为1的矩形; 俯视图:半径为1的圆 求此图形的体积 
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
二次函数图象的顶点在原点O,经过点A(1,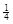 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.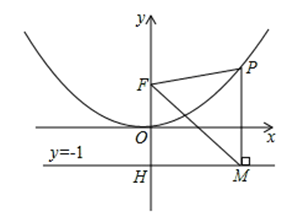
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
如图,AB是⊙O的直径,点F,C是⊙O上两点,且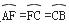 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2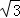 ,求⊙O的半径.
,求⊙O的半径.