(年山东淄博4分)如图,在正方形网格中有一边长为4的平行四边形ABCD,请将其剪拼成一个有一边长为6的矩形.(要求:在答题卡的图中画出裁剪线即可)
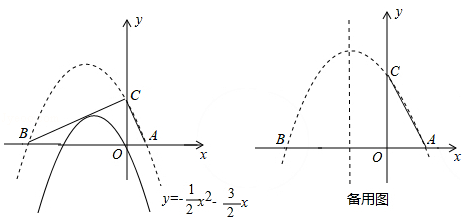
已知抛物线 y=﹣ x 2﹣ x的图象如图所示:
(1)将该抛物线向上平移2个单位,分别交 x轴于 A、 B两点,交 y轴于点 C,则平移后的解析式为 .
(2)判断△ ABC的形状,并说明理由.
(3)在抛物线对称轴上是否存在一点 P,使得以 A、 C、 P为顶点的三角形是等腰三角形?若存在,求出点 P的坐标;若不存在,说明理由.
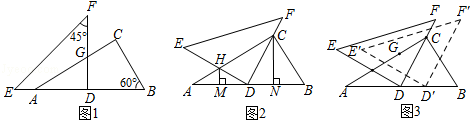
将一副三角尺按图1摆放,等腰直角三角尺的直角边 DF恰好垂直平分 AB,与 AC相交于点 G, BC=2 cm.
(1)求 GC的长;
(2)如图2,将△ DEF绕点 D顺时针旋转,使直角边 DF经过点 C,另一直角边 DE与 AC相交于点 H,分别过 H、 C作 AB的垂线,垂足分别为 M、 N,通过观察,猜想 MD与 ND的数量关系,并验证你的猜想.
(3)在(2)的条件下,将△ DEF沿 DB方向平移得到△ D′ E′ F′,当 D′ E′恰好经过(1)中的点 G时,请直接写出 DD′的长度.
阅读下列材料:
如图1,在△ ABC中,∠ A、∠ B、∠ C所对的边分别为 a、 b、 c,可以得到:
S △ ABC= absin C= acsin B= bcsin A
证明:过点 A作 AD⊥ BC,垂足为 D.
在Rt△ ABD中,sin B=
∴ AD= c•sin B
∴ S △ ABC= a• AD= acsin B
同理: S △ ABC= absin C
S △ ABC= bcsin A
∴ S △ ABC= absin C= acsin B= bcsin A
(1)通过上述材料证明:
(2)运用(1)中的结论解决问题:
如图2,在△ ABC中,∠ B=15°,∠ C=60°, AB=20 ,求 AC的长度.
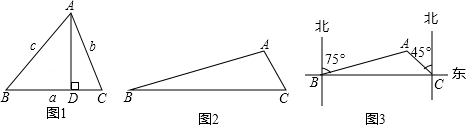
(3)如图3,为了开发公路旁的城市荒地,测量人员选择 A、 B、 C三个测量点,在 B点测得 A在北偏东75°方向上,沿笔直公路向正东方向行驶18 km到达 C点,测得 A在北偏西45°方向上,根据以上信息,求 A、 B、 C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9, ≈1.4,结果取整数)
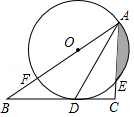
如图,在Rt△ ABC中,∠ C=90°, AD平分∠ BAC,交 BC于点 D,点 O在 AB上,⊙ O经过 A、 D两点,交 AC于点 E,交 AB于点 F.
(1)求证: BC是⊙ O的切线;
(2)若⊙ O的半径是2 cm, E是 的中点,求阴影部分的面积.(结果保留π和根号)
小明同学三次到某超市购买 A、 B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
|
类别 次数 |
购买 A商品数量(件) |
购买 B商品数量(件) |
消费金额(元) |
|
第一次 |
4 |
5 |
320 |
|
第二次 |
2 |
6 |
300 |
|
第三次 |
5 |
7 |
258 |
解答下列问题:
(1)第 次购买有折扣;
(2)求 A、 B两种商品的原价;
(3)若购买 A、 B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买 A、 B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买 A商品多少件.