（2014年江西南昌12分）如图1，抛物线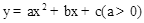的顶点为M，直线y-优题课

题文

（2014年江西南昌12分）如图1，抛物线的顶点为M，直线y=m与x轴平行，且与抛物线交于点A，B，若△AMB为等腰直角三角形，我们把抛物线上A、B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形，线段AB称为碟宽，顶点M称为碟顶，点M到线段AB的距离称为碟高．

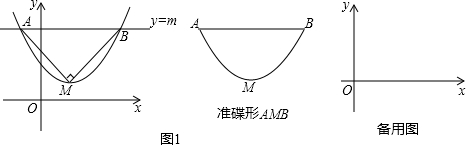
（1）抛物线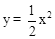对应的碟宽为；抛物线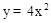对应的碟宽为；抛物线（a>0）对应的碟宽为；抛物线对应的碟宽；
（2）若抛物线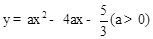对应的碟宽为6，且在x轴上，求a的值；
（3）将抛物线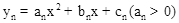的对应准蝶形记为F_n（n=1,2,3，…），定义F₁，F₂，…．．F_n为相似准蝶形，相应的碟宽之比即为相似比．若F_n与F_n-1的相似比为，且F_n的碟顶是F_n-1的碟宽的中点，现在将（2）中求得的抛物线记为y₁，其对应的准蝶形记为F₁．
①求抛物线y₂的表达式
② 若F₁的碟高为h₁,F₂的碟高为h₂，…F_n的碟高为h_n_。则h_n= ,F_n的碟宽右端点横坐标为；F₁，F₂，…．F_n的碟宽右端点是否在一条直线上？若是，直接写出改直线的表达式；若不是，请说明理由．

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

如图， $AB$ 为半圆 $O$ 的直径， $AC$ 是 $⊙ O$ 的一条弦， $D$ 为 $\hat{BC}$ 的中点，作 $DE ⊥ AC$ ，交 $AB$ 的延长线于点 $F$ ，连接 $DA$ ．

（1）求证： $EF$ 为半圆 $O$ 的切线；

（2）若 $DA = DF = 6 \sqrt{3}$ ，求阴影区域的面积．（结果保留根号和 $π)$

某蔬菜加工公司先后两批次收购蒜薹 $($ tái $)$ 共100吨．第一批蒜薹价格为4000元 $/$ 吨；因蒜薹大量上市，第二批价格跌至1000元 $/$ 吨．这两批蒜薹共用去16万元．

（1）求两批次购进蒜薹各多少吨？

（2）公司收购后对蒜薹进行加工，分为粗加工和精加工两种：粗加工每吨利润400元，精加工每吨利润1000元．要求精加工数量不多于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？

如图，某数学兴趣小组要测量一栋五层居民楼 $CD$ 的高度．该楼底层为车库，高2.5米；上面五层居住，每层高度相等．测角仪支架离地1.5米，在 $A$ 处测得五楼顶部点 $D$ 的仰角为 $60 °$ ，在 $B$ 处测得四楼顶部点 $E$ 的仰角为 $30 °$ ， $AB = 14$ 米．求居民楼的高度（精确到0.1米，参考数据： $\sqrt{3} \approx 1.73)$

某校为了解九年级男同学的体育考试准备情况，随机抽取部分男同学进行了1000米跑步测试．按照成绩分为优秀、良好、合格与不合格四个等级，学校绘制了如下不完整的统计图．

（1）根据给出的信息，补全两幅统计图；

（2）该校九年级有600名男生，请估计成绩未达到良好有多少名？

（3）某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛．预赛分别为 $A$ 、 $B$ 、 $C$ 三组进行，选手由抽签确定分组．甲、乙两人恰好分在同一组的概率是多少？

如图，已知抛物线 $y = a x^{2} + bx + c$ 过点 $A (- 1, 0)$ ， $B (3, 0)$ ， $C (0, 3)$ ，点 $M$ 、 $N$ 为抛物线上的动点，过点 $M$ 作 $MD / / y$ 轴，交直线 $BC$ 于点 $D$ ，交 $x$ 轴于点 $E$ ．

（1）求二次函数 $y = a x^{2} + bx + c$ 的表达式；

（2）过点 $N$ 作 $NF ⊥ x$ 轴，垂足为点 $F$ ，若四边形 $MNFE$ 为正方形（此处限定点 $M$ 在对称轴的右侧），求该正方形的面积；

（3）若 $∠ DMN = 90 °$ ， $MD = MN$ ，求点 $M$ 的横坐标．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号