如图，在边长为4的正方形ABCD中，动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动，动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动，动点E比动点F先出发1秒，其中一个动点到达终点时，另一个动点也随之停止运动，设点F的运动时间为t秒．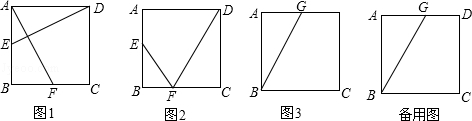
（1）点F在边BC上．
①如图1，连接DE，AF，若DE⊥AF，求t的值；
②如图2，连结EF，DF，当t为何值时，△EBF与△DCF相似？
（2）如图3，若点G是边AD的中点，BG，EF相交于点O，试探究：是否存在在某一时刻t，使得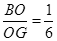
？若存在，求出t的值；若不存在，请说明理由．
正方形ABCD中，E点为BC中点，连接AE，过B点作BF⊥AE，交CD于F点，交AE于G点，连接GD，过A点作AH⊥GD交GD于H点．
(1) 求证：△ABE≌△BCF；
(2) 若正方形边长为4，AH =
，求△AGD的面积．
如图，直角梯形ABCD中，AD∥BC，∠A＝90°，AB＝AD＝6，DE⊥DC交AB于E，DF平分∠EDC交BC于F，连接EF．
（1） 证明：EF＝CF；
(2) 当AE＝2时，求EF的长．
如图，在□ABCD中，点E，F分别是BC和AD上的两点，且AE∥CF，延长AE与DC延长线交于点G，延长CF与BA的延长线交于点H，求证：HF = GE．
如图，是一块四边形花园ABDC，在一次数学课外实践活动中，小刚量得
，AC =" 3" m，AB =" 4" m，CD =
m，BD =" 10" m．求这个花园的面积．（结果保留整数，其中
）
如图，一次函数
的图象与反比例函数
的图象相交于点A
、B
．
求：(1) 求反比例函数和一次函数的解析式．
(2) 求直线AB与x轴的交点C的坐标及
的面积．
(3) 直接写出一次函数的值大于反比例函数的值的x的取值范围．