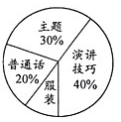
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形
(1)求该抛物线的解析式;
(2)求点P的坐标;
(3)求证:CE=EF;
(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+2 =
= ].
].
如图所示,将二次函数 的图象沿 轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数 的图象.函数 的图象的顶点为点 .函数 的图象的顶点为点 ,和 轴的交点为点 , (点 位于点 的左侧).
(1)求函数 的解析式;
(2)从点 , , 三个点中任取两个点和点 构造三角形,求构造的三角形是等腰三角形的概率;
(3)若点 是线段 上的动点,点 是 三边上的动点,是否存在以 为斜边的 ,使 的面积为 面积的 ?若存在,求 的值;若不存在,请说明理由.
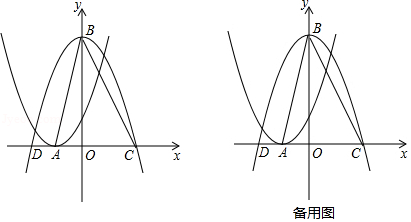
如图 1 所示, 在四边形 中, 点 , , , 分别是 , , , 的中点, 连接 , , , , .
(1) 证明: 四边形 是平行四边形;
(2) 将 绕点 顺时针旋转得到 ,如图 2 所示, 连接 , .
①若 , ,求 的值;
②试在四边形 中添加一个条件, 使 , 的长在旋转过程中始终相等 . (不 要求证明)
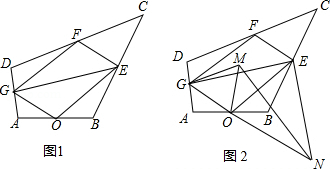
某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯 长为 ,坡角 为 ;改造后的斜坡式自动扶梯的坡角 为 ,请你计算改造后的斜坡式自动扶梯 的长度,(结果精确到0. ,温馨提示: ,
某公司计划购买 , 两种型号的机器人搬运材料.已知 型机器人比 型机器人每小时多搬运 材料,且 型机器人搬运 材料所用的时间与 型机器人搬运 材料所用的时间相同.
(1)求 , 两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购 , 两种型号的机器人共20台,要求每小时搬运材料不得少于 ,则至少购进 型机器人多少台?
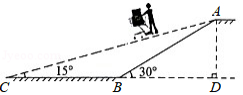
某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
|
项目 选手 |
服装 |
普通话 |
主题 |
演讲技巧 |
|
李明 |
85 |
70 |
80 |
85 |
|
张华 |
90 |
75 |
75 |
80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.