某公司计划购买 , 两种型号的机器人搬运材料.已知 型机器人比 型机器人每小时多搬运 材料,且 型机器人搬运 材料所用的时间与 型机器人搬运 材料所用的时间相同.
(1)求 , 两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购 , 两种型号的机器人共20台,要求每小时搬运材料不得少于 ,则至少购进 型机器人多少台?
计算或化简:
(1) 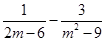 .(2)
.(2)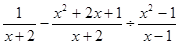
解不等式组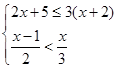 ,并写出它的整数解.
,并写出它的整数解.
如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.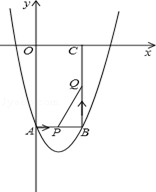
如图,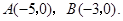 点
点 在
在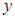 轴的正半轴上,
轴的正半轴上,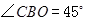 ,
,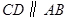 ,
,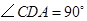 .点
.点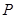 从点
从点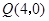 出发,沿
出发,沿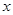 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为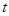 秒.
秒.
求点 的坐标;
的坐标;
当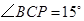 时,求
时,求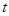 的值;
的值;
以点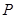 为圆心,
为圆心, 为半径的
为半径的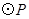 随点
随点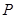 的运动而变化,当
的运动而变化,当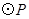 与四边形
与四边形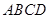
的边(或边所在的直线)相切时,求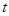 的值.
的值.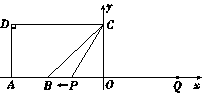
|
随着梅雨季节的临近,雨伞成为热销品.某景区与某制伞厂签订2万把雨伞的订购合同.合同规定:每把雨伞的出厂价为13元.景区要求厂方10天内完成生产任务,如果每延误1天厂方须赔付合同总价的1%给景区.由于急需,景区也特别承诺,如果每提前一天完成,每把雨伞的出厂价可提高0.1元.
⑴如果制伞厂确保在第10天完成生产任务,平均每天应生产雨伞把;
⑵生产2天后,制伞厂又从其它部门抽调了10名工人参加雨伞生产,同时,通过技术革新等手段使每位工人的工作效率比原计划提高了25%,结果提前2天完成了生产任务.求该厂原计划安排多少名工人生产雨伞?
⑶已知每位工人每天平均工资为60元,每把雨伞的材料费用为8.2元.如果制伞厂按照⑵中的生产方式履行合同,将获得毛利润多少元?(毛利润=雨伞的销售价-雨伞的材料费-工人工资)