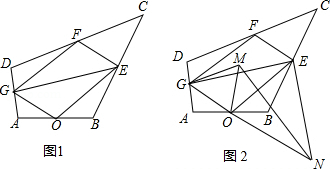
如图 1 所示, 在四边形 中, 点 , , , 分别是 , , , 的中点, 连接 , , , , .
(1) 证明: 四边形 是平行四边形;
(2) 将 绕点 顺时针旋转得到 ,如图 2 所示, 连接 , .
①若 , ,求 的值;
②试在四边形 中添加一个条件, 使 , 的长在旋转过程中始终相等 . (不 要求证明)
在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).
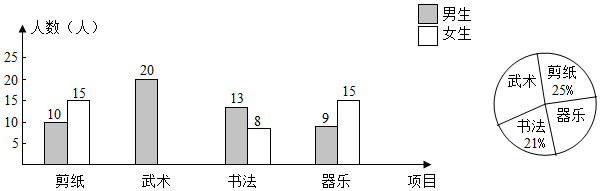
请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

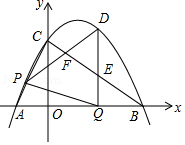
如图,一次函数 的图象分别与 轴, 轴相交于点 , ,与反比例函数 的图象相交于点 , .
(1)求一次函数和反比例函数的表达式;
(2)当 为何值时, ;
(3)当 为何值时, ,请直接写出 的取值范围.

如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),与 轴交于点 ,连接 、 .点 沿 以每秒1个单位长度的速度由点 向点 运动,同时,点 沿 以每秒2个单位长度的速度由点 向点 运动,当一个点停止运动时,另一个点也随之停止运动,连接 .过点 作 轴,与抛物线交于点 ,与 交于点 ,连接 ,与 交于点 .设点 的运动时间为 秒 .
(1)求直线 的函数表达式;
(2)①直接写出 , 两点的坐标(用含 的代数式表示,结果需化简)
②在点 、 运动的过程中,当 时,求 的值;
(3)试探究在点 , 运动的过程中,是否存在某一时刻,使得点 为 的中点?若存在,请直接写出此时 的值与点 的坐标;若不存在,请说明理由.
综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为 的三角形称为 ,4, 型三角形,例如:三边长分别为9,12,15或 , , 的三角形就是 ,4, 型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片 中, , .
第一步:如图2,将图1中的矩形纸片 沿过点 的直线折叠,使点 落在 上的点 处,折痕为 ,再沿 折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点 与点 重合,折痕为 ,然后展平,隐去 .
第三步:如图4,将图3中的矩形纸片沿 折叠,得到△ ,再沿 折叠,折痕为 , 与折痕 交于点 ,然后展平.
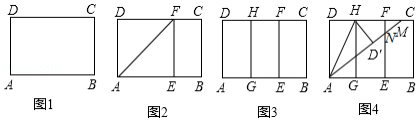
问题解决
(1)请在图2中证明四边形 是正方形.
(2)请在图4中判断 与 的数量关系,并加以证明;
(3)请在图4中证明 ,4, 型三角形;
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角形是 ,4, 型三角形?请找出并直接写出它们的名称.
如图, 内接于 ,且 为 的直径, ,与 交于点 ,与过点 的 的切线交于点 .
(1)若 , ,求 的长.
(2)试判断 与 的数量关系,并说明理由.
