如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点B(8,0),A(0,6),点C的坐标为(3,0),过点C作CE⊥AB于点E,点D为y轴上一动点,连结CD,DE,以CD,DE为边作□CDEF。是否存在点D,使□CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由。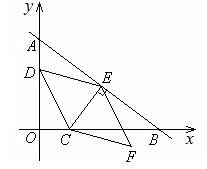
计算: .
.
如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+ x +c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
x +c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N。
①若直线l⊥BD,如图1所示,试求 的值;
的值;
②若l为满足条件的任意直线。如图2所示,①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例。
如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G。
(1)求证:AF⊥BE;
(2)试探究线段AO、BO、GO的长度之间的数量关系;
(3)若GO:CF=4:5,试确定E点的位置。
某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择。
方案一:每克种子价格为4元,无论购买多少均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次性购买超过3千克的,则超过3千克的部分的,则超过3千克的部分的种子价格打7折。
(1)请分别求出方案一和方案二中购买的种子数量x(千克)和付款金额.y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由。
已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。