如图,在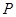 地正西方向
地正西方向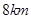 的
的 处和正东方向
处和正东方向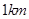 的
的 处各一条正北方向的公路
处各一条正北方向的公路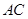 和
和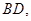 现计划在
现计划在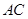 和
和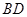 路边各修建一个物流中心
路边各修建一个物流中心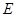 和
和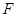 .为缓解交通压力,决定修建两条互相垂直的公路
.为缓解交通压力,决定修建两条互相垂直的公路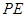 和
和 设
设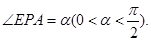
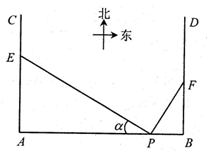
(1)为减少周边区域的影响,试确定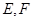 的位置,使△
的位置,使△ 与△
与△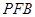 的面积之和最小;
的面积之和最小;
(2)为节省建设成本,试确定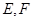 的位置,使
的位置,使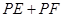 的值最小.
的值最小.
已知
,函数
,记
为
的从小到大的第
(
)个极值点,证明:
(1)数列
是等比数列
(2)若
,则对一切
,
恒成立.
已知抛物线
的焦点
也是椭圆
的一个焦点,
与
的公共弦的长为
.
(1)求
的方程;
(2)过点
的直线
与
相交于
两点,与
相交于
两点,且
与
同向
(ⅰ)若
,求直线
的斜率
(ⅱ)设
在点
处的切线与
轴的交点为
,证明:直线
绕点
旋转时,
总是钝角三角形
如图,已知四棱台
上、下底面分别是边长为3和6的正方形,
,且
底面
,点
分别在棱
上.

(1)若
是
的中点,证明:
;
(2)若
平面
,二面角
的余弦值为
,求四面体
的体积.
某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
,求
的分布列和数学期望.
设
的内角
的对边分别为
,且
为钝角.
(1)证明:
;
(2)求
的取值范围.