已知数列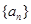 的前
的前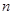 项和为
项和为 ,且满足
,且满足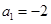 ,
,
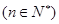 .
.
(1)求数列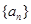 的通项公式;
的通项公式;
(2)是否存在整数对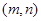 ,使得等式
,使得等式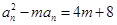 成立?若存在,请求出所有满足条件的
成立?若存在,请求出所有满足条件的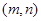 ;若不存在,请说明理由.
;若不存在,请说明理由.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点 ,求|MA|·|MB|.
,求|MA|·|MB|.
已知函数f(x)=2ax- -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).
(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2,3),x1,x2∈[1,3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围。
已知 是椭圆E:
是椭圆E: 的两个焦点,抛物线
的两个焦点,抛物线 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y= 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
(1)求椭圆E的方程;
(2)如图,过点 的动直线
的动直线 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.879 |
10.828 |
附:
若 的图像与直线
的图像与直线 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为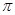 的等差数列.
的等差数列.
(1)求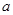 和
和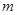 的值;
的值;
(2)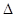 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若 是函数
是函数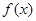 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求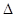 ABC面积的最大值.
ABC面积的最大值.