如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题:
(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2011年到2015年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人.A旅游点决定提高门票价格来控制游客数量.已知游客数量y(万人)与门票价格x(元)之间满足函数关系y=5- .若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
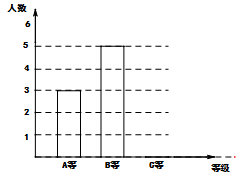
(·湖南株洲)某学校举行一次体育测试,从所有参加测试的学生中随机抽取10名学生的成绩,制作出如下统计表和条形统计图:
| 编号 |
成绩 |
等级 |
编号 |
成绩 |
等级 |
| 95 |
A |
⑥ |
76 |
B |
|
| 78 |
B |
⑦ |
85 |
A |
|
| 72 |
C |
⑧ |
82 |
B |
|
| 79 |
B |
⑨ |
77 |
B |
|
| 92 |
A |
⑩ |
69 |
C |
请回答下列问题:
(1)孔明同学这次测试的成绩是87分,则他的成绩等级是 ;
(2)请将条形统计图补充完整;
(3)已知该校所有参加这次测试的学生中,有60名学生成绩是A等,请根据以上抽样结果,估计该校参加这次测试的学生总人数是多少?
(·湖南益阳)2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题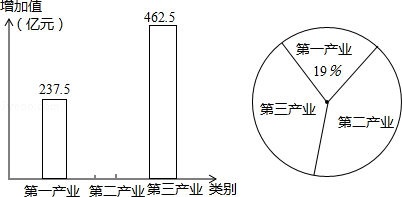
(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.
(·湖南长沙)中华文明,源远流长:中华汉字,寓意深广。为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分。为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
请根据所给的信息,解答下列问题:
a= ,b= ;
请补全频数分布直方图;
这次比赛成绩的中位数会落在 分数段;
若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的大约有多少人?
(·湖南常德)某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果分别绘制了如下两个统计图。请根据图中提供的信息解答下列问题:

(1)图1中,“吸烟”类人数所占扇形的圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图
(4)若该市共有市民760万人,求该市大约有多少人吸烟?
(·湖南常德)商场为了促销某件商品,设置了如图的一个转盘,它被分成了3个相同的扇形。各扇形分别标有数字2,3,4,指针的位置固定,该商品的价格由顾客自由转动此转盘两次来获取,每次转动后让其自由停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?