如图1，已知矩形纸片ABCD中，AB＝6cm，若将该纸片沿着过点B的直线折叠（折痕为BM），点A恰好落在CD边的中点P处．
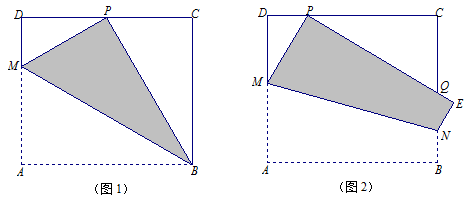
（1）求矩形ABCD的边AD的长．
（2）若P为CD边上的一个动点，折叠纸片，使得A与P重合，折痕为MN，其中M在边AD上，N在边BC上，如图2所示．设DP＝x cm，DM＝y cm，试求y与x的函数关系式，并指出自变量x的取值范围．
（3）①当折痕MN的端点N在AB上时，求当△PCN为等腰三角形时x的值；
②当折痕MN的端点M在CD上时，设折叠后重叠部分的面积为S，试求S与x之间的函数关系式
某学校初三年级男生共200人，随机抽取10名测量他们的身高为（单位：cm）：
181、176、169、155、163、175、173、167、165、166．
（1）求这10名男生的平均身高和上面这组数据的中位数；
（2）估计该校初三年级男生身高高于170cm的人数；
（3）从身高为181、176、175、173的男生中任选2名，求身高为181cm的男生被抽中的概率．
如图，是一副学生用的三角板，在△ABC 中，∠C=90°， ∠A=60°，∠B=30°；在△
中，∠C
=90°， ∠A=45°，∠B=45°，且AB
=" CB" ．若将边
与边CA重合，其中点
与点C重合．将三角板绕点C（）按逆时针方向旋转，旋转过的角为
，旋转过程中边与边AB的交点为M， 设AC=
．
（1）计算的长；
（2）当=30°时，证明：
∥AB；
（3）若=
，当=45°时，计算两个三角板重叠部分图形的面积；
（4）当=60°时，用含的代数式表示两个三角板重叠部分图形的面积．
（参考数据：
°= 
，
°= 
，
°=
°= ， 
°= ， 
°=
）
某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计，得到如下数据：
| 单价（元/件） |
30 |
34 |
38 |
40 |
42 |
| 销量（件） |
40 |
32 |
24 |
20 |
16 |
（1）计算这5天销售额的平均数（销售额=单价
销量）
（2）通过对上面表格中的数据进行分析，发现销量
（件）与单价
（元/件）之间存在一次函数关系，求关于的函数关系式（不需要写出函数自变量的取值范围）；
（3）预计在今后的销售中，销量与单价仍然存在（2）中的关系，且该产品的成本是20元/件．为使工厂获得最大利润，该产品的单价应定为多少?
已知点A 
在抛物线
的图象上，设点A关于抛物线对称轴对称的点为B．
（1）求点B的坐标；
（2）求
度数．
如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，
．
（1）求证：PB是
的切线；
（2）连接OP，若
，且OP=8，的半径为
，求BC的长．