如图,是一副学生用的三角板,在△ABC 中,∠C=90°, ∠A=60°,∠B=30°;在△ 中,∠C
中,∠C =90°, ∠A
=90°, ∠A =45°,∠B
=45°,∠B =45°,且A
=45°,且A B
B =" CB" .若将边
=" CB" .若将边 与边CA重合,其中点
与边CA重合,其中点 与点C重合.将三角板
与点C重合.将三角板 绕点C(
绕点C( )按逆时针方向旋转,旋转过的角为
)按逆时针方向旋转,旋转过的角为 ,旋转过程中边
,旋转过程中边 与边AB的交点为M, 设AC=
与边AB的交点为M, 设AC= .
.
(1)计算 的长;
的长;
(2)当 =30°时,证明:
=30°时,证明: ∥AB;
∥AB;
(3)若 =
= ,当
,当 =45°时,计算两个三角板重叠部分图形的面积;
=45°时,计算两个三角板重叠部分图形的面积;
(4)当 =60°时,用含
=60°时,用含 的代数式表示两个三角板重叠部分图形的面积.
的代数式表示两个三角板重叠部分图形的面积.
(参考数据: °=
°=  ,
, °=
°=  ,
, °=
°=
 °=
°=  ,
,  °=
°=  ,
,  °=
°= )
)
解方程: .
.
如图,一次函数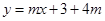 (m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(1)用含m的代数式分别表示点B,点E的坐标;
(2)若△ABC中AC边上的高为5,求m的值;
(3)若点P为线段AC中点,是否存在m的值,使△APD与△ABD相似?若存在,请求出m的值;若不存在,请说明理由.
如图,矩形ABCD中, AB=4,BC=2,点P是射线DA上的一动点,DE⊥CP,垂足为E,EF⊥BE与射线DC交于点F.
(1)若点P在边DA上(与点D、点A不重合).
①求证:△DEF∽△CEB;
②设AP=x,DF=y,求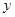 与
与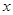 的函数关系式,并写出
的函数关系式,并写出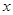 的取值范围;
的取值范围;
(2)当△EFC与△BEC面积之比为3︰16时,线段AP的长为多少?(直接写出答案,不必说明理由).
已知二次函数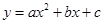 中,其函数
中,其函数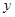 与自变量
与自变量 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:
| x |
…… |
0 |
1 |
2 |
3 |
4 |
5 |
…… |
| y |
…… |
4 |
1 |
0 |
1 |
4 |
9 |
…… |
(1)当x=-1时,y的值为;
(2)点A(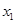 ,
, )、B(
)、B(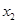 ,
,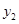 )在该函数的图象上,则当
)在该函数的图象上,则当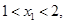
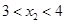 时,
时, 与
与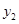 的大小关系是;
的大小关系是;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式:;
(4)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)都在二次函数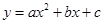 的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
五一假期中,小明和小亮相约晨练跑步.小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮.两人沿滨江路并行跑了2分钟后,决定进行直线长跑比赛,比赛时小明的速度始终是250米/分,小亮的速度始终是300米/分.下图是两人之间的距离y(米)与小明离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
(1)请直接写出小明和小亮比赛前的速度,并说出图中点A(1,500)的实际意义;
(2)请在图中的()内填上正确的值,并求两人比赛过程中y与x之间的函数关系式;
(3)若小亮从家出门跑了11分钟时,立即按原路以比赛时的速度返回,则小亮再经过多少分钟时两人相距75米?