(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为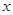 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线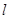 的参数方程是
的参数方程是 (
( 为参数).
为参数).
(1)求曲线 的直角坐标方程与直线
的直角坐标方程与直线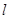 的普通方程;
的普通方程;
(2)设点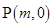 ,若直线
,若直线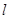 与曲线
与曲线 交于
交于 ,
,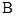 两点,且
两点,且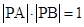 ,求实数
,求实数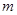 的值.[来
的值.[来
已知函数 图象上一点
图象上一点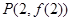 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若方程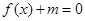 在
在 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数).
为自然对数的底数).
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF  平面ABCD,BF=3,G,H分别是CE和CF的中点、
平面ABCD,BF=3,G,H分别是CE和CF的中点、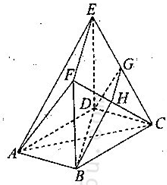
(1)求证:AF//平面BDGH:
(2)求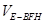
数列 的前n项和为
的前n项和为 。
。
(1)求数列 的通项公式;
的通项公式;
(2)等差数列 的各项为正,
的各项为正, ,又
,又 成等比数列,若
成等比数列,若 ,求
,求 的前
的前 项和
项和 。
。
如图,四棱锥P﹣ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
(1)求证:平面PAD与平面PAB垂直;
(2)求直线PC与直线AB所成角的余弦值.
在锐角△ABC中,角A,B,C的对边分别为 .已知
.已知 .
.
(1)求B;
(2)若 ,
, ,求
,求 .
.