如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,
又棱PA=AB=2,E为CD的中点,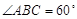 .
.
(Ⅰ)求证:直线EA⊥平面PAB;
(Ⅱ)求直线AE与平面PCD所成角的正切值.
某化工厂生产的某种化工产品,当年产量在150吨至250吨之内,其年生产的
总成本 (万元)与年产量
(万元)与年产量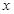 (吨)之间的关系可近似地表示为
(吨)之间的关系可近似地表示为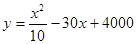
(1)当年产量为多少吨时,每吨的平均成本最低,并求每吨最低平均成本;
(2)若每吨平均出厂价为16万元,求年生产多少吨时,可获得最大的年利润,并求最大年
利润.
已知数列{an}的前n项和为Sn,且满足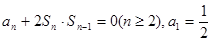
(Ⅰ)求证:{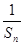 }是等差数列;
}是等差数列;
(Ⅱ)求an的表达式
如图,已知四棱锥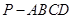 的底面
的底面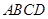 是菱形,
是菱形,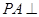 平面
平面 ,
,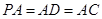 ,点
,点 为
为 的中点.
的中点.
(Ⅰ)求证: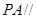 平面
平面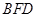 ;
;
(Ⅱ)求二面角 的正切值.
的正切值.
已知函数 在同一周期内有最高点
在同一周期内有最高点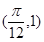 和最低点
和最低点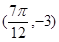 ,(1)求此函数
,(1)求此函数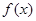 的解析式;(2)函数
的解析式;(2)函数 的图像如何由函数
的图像如何由函数 的图像变换得到?
的图像变换得到?
如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)79.5到89.5这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率( 分及以上为及格).
分及以上为及格).