已知函数 ,
,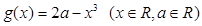
(1)求函数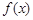 的单调区间;
的单调区间;
(2)求函数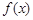 的极值;
的极值;
(3)若任意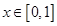 ,不等式
,不等式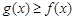 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知函数
(I)求函数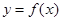 图象的对称轴方程;
图象的对称轴方程;
(II)求函数 的最小正周期和值域.
的最小正周期和值域.
(本小题满分10分)设函数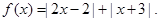
(I)解不等式 ;
;
(II)若关于x的不等式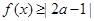 恒成立,试求a的取值范围.
恒成立,试求a的取值范围.
已知函数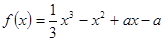 (
(
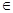 R).
R).
(1) 当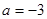 时,求函数
时,求函数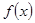 的极值;
的极值;
(2)若函数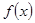 的图象与
的图象与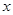 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.
(本小题满分14分)
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
…… … …
…… … ……
假设第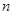 行的第二个数为
行的第二个数为 ,
,
(Ⅰ)依次写出第六行的所有 个数字;
个数字;
(Ⅱ)归纳出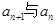 的关系式并求出
的关系式并求出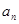 的通项公式;
的通项公式;
(Ⅲ)设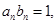 求证:
求证:
(本小题满分14分)
设椭圆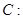
 的离心率为
的离心率为 =
=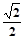 ,点
,点 是椭圆上的一点,
是椭圆上的一点,
且点 到椭圆
到椭圆 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆 的方程;
的方程;
(2)椭圆 上一动点
上一动点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
求 的取值范围.
的取值范围.