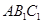已知椭圆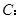
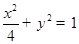 ,
,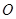 为坐标原点,直线
为坐标原点,直线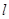 与椭圆
与椭圆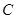 交于
交于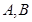 两点,且
两点,且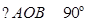 .
.
(Ⅰ)若直线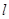 平行于
平行于 轴,求
轴,求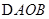 的面积;
的面积;
(Ⅱ)若直线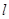 始终与圆
始终与圆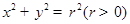 相切,求
相切,求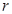 的值.
的值.
(本小题满分13分)已知函数簇 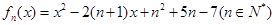 .
.
(1)设曲线列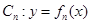 的顶点的纵坐标构成数列
的顶点的纵坐标构成数列 ,求证:数列
,求证:数列 为等差数列;
为等差数列;
(2)设曲线列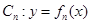 的顶点到
的顶点到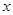 轴的距离构成数列
轴的距离构成数列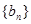 ,
, 为数列
为数列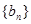 的前
的前 项和,求S20.
项和,求S20.
如图,已知 平面
平面 ,
, 于D,
于D, 。
。
(Ⅰ)令 ,
, ,试把
,试把 表示为
表示为 的函数,并求其最大值;
的函数,并求其最大值;
(Ⅱ)在直线PA上是否存在一点Q,使得 ?
?
将一个长、宽分别 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,
(Ⅰ)设切去小正方形的边长为 ,用
,用 表示这个长方体的外接球的半径
表示这个长方体的外接球的半径 ;
;
(Ⅱ)若这个长方体的外接球的体积存在最小值,求 的取值范围.
的取值范围.
(本小题满分10分)如图,四棱锥 的底面是正方形,
的底面是正方形,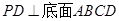 ,点
,点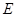 在棱
在棱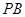 上.
上.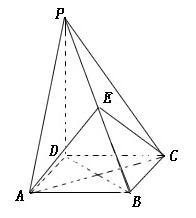
(Ⅰ)求证:平面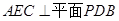 ;
;
(Ⅱ)当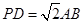 且
且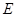 为
为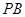 的中点时,求
的中点时,求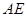 与平面
与平面 所成的角的大小.
所成的角的大小.
(本小题满分10分)如图所示,在三棱柱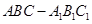 中,
中,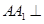 平面
平面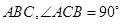 ,
,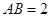 ,
,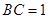 ,
,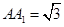 .
.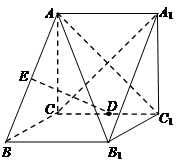
(Ⅰ)求三棱锥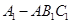 的体积;
的体积;
(Ⅱ)若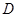 是棱
是棱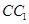 的中点,
的中点,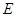 为
为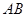 的中点,证明
的中点,证明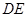 平行平面
平行平面