（本小题满分12分）如图，点C是以AB为直径的圆O上不与A、B重合的一个动点，S是圆O所在平面外一点，且总有SC⊥平面ABC，M是SB的中点，AB=SC=2．
（Ⅰ）求证：OM⊥BC；
（Ⅱ）当四面体S－ABC的体积最大时，设直线AM与平面ABC所成的角为
，二面角B－SA－C的大小为
，分别求
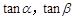的值．
（本小题满分14分）
已知定义域为R的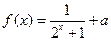函数
为奇函数。
（1）求a的值.
（2）证明函数f(x)在R上是减函数.
（3)若不等式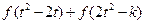
<0对任意的实数t 恒成立，求k的取值范围.
(本小题满分14分)
在
中，角A、B、C的对边分别为a、b、c，且
，
，
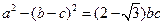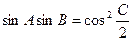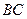边上的中线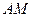
的长为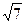
．
(Ⅰ) 求角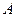
和角
的大小； (Ⅱ) 求的面积．
已知点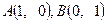
,
.
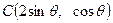（Ⅰ）若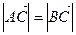
, 求
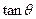的值;
（Ⅱ）设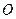
为坐标原点, 点C在第一象限, 求函数
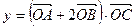的单调递增区间与值域.
设函数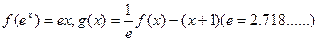
（1）求函数g(x)的极大值
（2）求证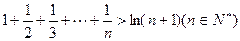
(3)若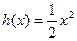
，曲线y=
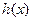与 y=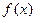
是否存在公共点，若存在公共点，在公共点处是否存在公切线，若存在，求出公切线方程，若不存在，说明理由。
已知函数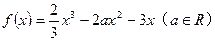
(1)若函数y=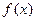
在（-1,1）内是减函数，求
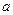的取值范围
(2)若函数y=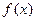在（-1,1）内有且只有一个极值点，求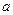的取值范围