(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是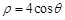 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
(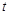 是参数).
是参数).
(Ⅰ)若直线l与曲线C相交于A、B两点,且 ,试求实数m值.
,试求实数m值.
(Ⅱ)设 为曲线
为曲线 上任意一点,求
上任意一点,求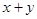 的取值范围.
的取值范围.
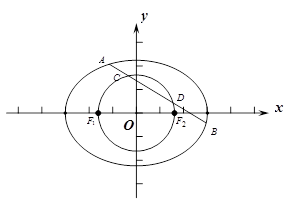
已知椭圆
经过点
,离心率为
,左右焦点分别为
.
(1)求椭圆的方程;
(2)若直线
与椭圆交于
两点,与以
为直径的圆交于
两点,且满足
,求直线
的方程.
某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
| 赔付金额(元) |
0 |
1000 |
2000 |
3000 |
4000 |
| 车辆数(辆) |
500 |
130 |
100 |
150 |
120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10℅,在赔付金额为4000元的样本车辆中,车主是新司机的占20℅,估计在已投保车辆中,新司机获赔金额为4000元的概率.
在直角坐标系
中,已知点
,点
在
三边围成的区域(含边界)上,且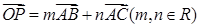
(1)若
,求
;
(2)用
表示
,并求
的最大值.
四面体
及其三视图如图所示,平行于棱
的平面分别交四面体的棱
于点
.
(1)求四面体
的体积;
(2)证明:四边形
是矩形.
的内角
所对的边分别为
.
(1)若
成等差数列,证明:
;
(2)若
成等比数列,且
,求
的值.