在某校对30名女生与80名男生进行是否有懒惰习惯进行调查,发现女生中有15人有懒惰习惯,男生中有50人有懒惰习惯。
(1)请根据上述数据填写2×2列联表;
| |
懒惰 |
不懒惰 |
总计 |
| 女 |
|
|
|
| 男 |
|
|
|
| 总计 |
|
|
|
(2)能否判断懒惰是否与性别有关。(参考公式: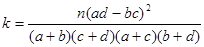 )
)
临界值表
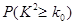 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分10分)选修4-1:几何证明选讲
已知在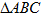 中,
中,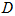 是
是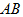 上一点,
上一点, 的外接圆交
的外接圆交 于
于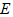 ,
, .
.
(1)求证: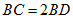 ;
;
(2)若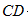 平分
平分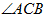 ,且
,且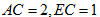 ,求
,求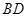 的长.
的长.
设函数 ,曲线
,曲线 过点P(1,0),且在P点处的切线的斜率为2,
过点P(1,0),且在P点处的切线的斜率为2,
(1)求 的值。
的值。
(2)证明:
(本小题满分12分)已知直线 与椭圆
与椭圆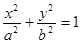
 相交于
相交于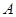 、
、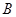 两点.
两点.
(1)若椭圆的离心率为 ,焦距为
,焦距为 ,求线段
,求线段 的长;
的长;
(2)若向量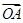 与向量
与向量 互相垂直(其中
互相垂直(其中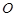 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率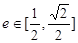 时,求椭圆长轴长的最大值.
时,求椭圆长轴长的最大值.
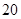 名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
(1)求频率分布直方图中 的值;
的值;
(2)分别求出成绩落在 与
与 中的学生人数;
中的学生人数;
(3)从成绩在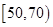 的学生中任选
的学生中任选 人,求此
人,求此 人的成绩都在
人的成绩都在 中的概率.
中的概率.
如图,在四棱锥 中,底面
中,底面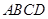 是
是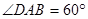 且边长为
且边长为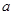 的菱形,侧面
的菱形,侧面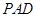 是等边三角形,且平面
是等边三角形,且平面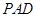 ⊥底面
⊥底面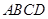 ,
,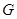 为
为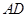 的中点.
的中点.
(1)求证: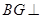 平面
平面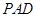 ;
;
(2)求 点G到平面PAB的距离。