设a,b,c,d均为正数，且abcd，证明：（Ⅰ）若ab<c-优题课

设 $a, b, c, d$ 均为正数，且 $a + b = c + d$ ，证明：
（Ⅰ）若 $a b > c d$ ，则 $\sqrt{a} + \sqrt{b} > \sqrt{c} + \sqrt{d}$ ；
（Ⅱ） $\sqrt{a} + \sqrt{b} > \sqrt{c} + \sqrt{d}$ 是 $| a - b | < | c - d |$ 的充要条件．

科目数学题型解答题难度中等

（本小题满分12分）袋中有大小、形状相同的红、黑球各一个，现一次有放回地随机摸取3次，每次摸取一个球。（I）试问：一共有多少种不同的结果？请列出所有可能的结果；（Ⅱ）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率。

人造卫星的运行轨道是以地球的中心为一个焦点的椭圆，近地点离地面距离为p，远地点离地面距离为q，地球的半径为R．求卫星运行轨道的短轴长．

抛物线y²＝2px的焦点弦AB的中点为M，A、B、M在准线上的
影依次为C、D、N．求证：
(1)A、O、D三点共线，B、O、C三点共线；
(2)FN⊥AB(F为抛物线的焦点)

．已知双曲线＝1(a＞0，b＞0)的左、右两个焦点分别为F₁、F₂，P是它左支上一点，P到左准线的距离为d，双曲线的一条渐近线为y＝x，问是否存在点P，使｜PF₁｜、｜PF₂｜成等比数列？若存在，求出P的坐标；若不存在说明理由．

求所有的正整数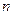，使得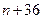是一个完全平方数，且除了2或3以外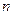，没有其他的质因数.

试卷网试题网古诗词网作文网范文网