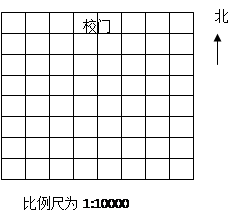已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(一2,2).现将△ABC平移,使点A变换为点A′,点B′,C′分别是B,C的对应点.
(1)请画出平移后的图像△A′B′C′(不写画法),并直接写出点B′,C′的坐标:B′( )、C′( );
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ).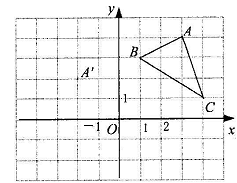
.如图,已知 ,求
,求 的度数.
的度数.
问题情景::狼山水上乐园门票价格如下表所示:
| 购票人数 |
1~50人 |
51~100人 |
100人以上 |
| 每人门票价 |
13元 |
11元 |
9元 |
某校七年级(1),(2)两个班共104人去狼山水上乐园春游,其中(1)班人数较少,不到50人,(2)班人数较多,超过50人.经估算如果两班都以班为单位分别购票,则一共应付1240元。
问题:(1)请算出两个班各有多少名学生?
(2)想一想:你认为他们如何购票比较合算?
(3) (1)班先到达乐园,想要单独购票,你能帮他们想出一个比较经济的购票方案吗?
如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a、b的值。
解:(1)A:____,D:_____B:____,
E:____,C:____,F:_____
特征:________________________________
(2)
小明写信给他的朋友,介绍他学校的有关情况:学校的校门在北侧,进校门向南走50米是旗杆,再向南走100米是教学楼.从教学楼向东走150米,再向北走50米是图书馆.从教学楼向西走100米,再向南走150米是实验楼.现已知校门的位置,图中的单位长度是0.5cm.请建立适当的坐标系,标出旗杆、教学楼、图书馆、实验楼的位置,并写出它们的坐标.